题目内容

13．湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个半径为4cm，深2cm的空穴，则该球表面积为（　　） cm2．
A．400πB．300πC．200πD．100π

分析 设球的半径为Rcm，根据题意可得冰面到球心的距离为（R-2）cm，冰面截球得到的小圆半径为4cm，利用勾股定理建立关于R的方程，解出R，再根据球的表面积公式即可算出该球的表面积

解答 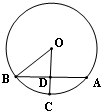解：设球心为O，OC是与冰面垂直的一条球半径，
冰面截球得到的小圆圆心为D，AB为小圆D的一条直径，
设球的半径为Rcm，则CD=R-OD=2cm，
∴Rt△OBD中，OB=Rcm，OD=（R-2）cm，BD=4cm．
根据勾股定理，得OD2+BD2=OB2，
即（R-2）2+42=R2，解之得R=5cm，
∴该球表面积为S=4πR2=4π×52=100π．
故选：D．

点评 本题给出实际问题，求冰面上的球的表面积．着重考查了球的截面圆性质、勾股定理和球的表面积计算等知识，属于基础题．

练习册系列答案
相关题目
3．正四棱锥P-ABCD的侧棱长为$\sqrt{5}$，底面ABCD边长为2，E为AD的中点，则BD与PE所成角的余弦值为（　　）
A．$\frac{{\sqrt{2}}}{4}$B．$\frac{1}{3}$C．$\frac{{\sqrt{3}}}{4}$D．$\frac{{\sqrt{6}}}{4}$
4．若圆（x-3）2+y2=1上只有一点到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离为1，则该双曲线离心率为（　　）
A．$\frac{{3\sqrt{5}}}{5}$B．$\frac{{3\sqrt{3}}}{4}$C．$\sqrt{3}$D．$\sqrt{5}$
1．若非零向量$\overrightarrow a$，$\overrightarrow b$满足$\overrightarrow{a}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=0，2|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则向量$\overrightarrow a$，$\overrightarrow b$夹角的大小为120°．
8．已知椭圆G：$\frac{{x}^{2}}{2}$+y2=1，与x轴不重合的直线l经过左焦点F1，且与椭圆G相交于A，B两点，弦AB的中点为M，直线OM与椭圆G相交于C，D两点．
（1）若直线l的斜率为1，求直线OM的斜率；
（2）是否存在直线l，使得|AM|2=|CM|•|DM|成立？若存在，求出直线l的方程；若不存在，请说明理由．
18．焦点在（-2，0）和（2，0），经过点（2，3）的椭圆方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$．
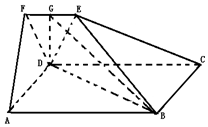5．如图，在五面体ABCDEF中，四边形ABCD为正方形，EF∥CD，平面CDFE⊥平面ABCD，且AD=3EF，DE=DF，点G为EF中点．
（Ⅰ）求证：DG⊥BC；
（Ⅱ）M是线段BD上一点，若GM∥平面ADF，求DM：MB的值．
2．已知圆锥的底面半径和高均为1，则该圆锥的侧面积为$\sqrt{2}π$．
3．设数列{an}的前n项和为Sn，若Sn+1=2an+1，n∈N*，则a3=（　　）
A．3B．2C．1D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网