题目内容
16.甲、乙、丙、丁、戊五人排成一排,甲和乙都排在丙的同一侧,排法种数为( )| A. | 12 | B. | 40 | C. | 60 | D. | 80 |
分析 根据题意,分①甲和乙都排在丙的左侧和②甲和乙都排在丙的右侧两种情况讨论,分别求出每种情况下的排法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、甲和乙都排在丙的左侧,
将甲乙安排在丙的左侧,考虑甲乙之间的顺序,有2种情况,排好后有4个空位,
在4个空位中选一个安排丁,有4种情况,排好后有5个空位,
在5个空位中选一个安排戊,有5种情况,
则甲和乙都排在丙的左侧的情况有2×4×5=40种,
②、甲和乙都排在丙的右侧,同理有40种不同的排法;
故甲和乙都排在丙的同一侧的排法种数为40+40=80种;
故选:D.
点评 本题考查排列、组合的应用,涉及分步、分类计数原理的应用,

练习册系列答案
相关题目
7.要得到y=cos2x-1的图象,只需将函数y=sin2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| C. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 | |
| D. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 |
4.若圆(x-3)2+y2=1上只有一点到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离为1,则该双曲线离心率为( )
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
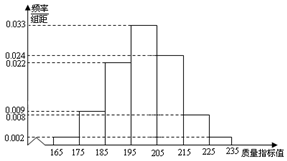 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).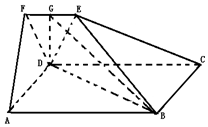 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.