题目内容
已知点O为坐标原点，点M（2，-1），点N（x，y）满足不等式组
，则
•
的最大值为 ．
|
| OM |
| ON |
考点：简单线性规划,平面向量数量积的运算
专题：计算题,作图题,不等式的解法及应用
分析：由题意作出其平面区域，
=（2，-1）•
=（x，y），令z=
•
=2x-y化为y=2x-z，-z相当于直线y=y=2x-z的纵截距，由几何意义可得．
| OM |
| ON |
| OM |
| ON |
解答：
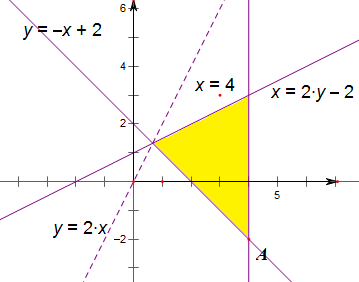
解：由题意作出其平面区域，
=（2，-1）•
=（x，y），
令z=
•
=2x-y化为y=2x-z，
-z相当于直线y=y=2x-z的纵截距，
则过点A时有最大值，
由x=4与x+y=2解得，A（4，-2），
故
•
的最大值为2×4+2=10，
故答案为：10．
| OM |
| ON |
令z=
| OM |
| ON |
-z相当于直线y=y=2x-z的纵截距，
则过点A时有最大值，
由x=4与x+y=2解得，A（4，-2），
故
| OM |
| ON |
故答案为：10．
点评：本题考查了简单线性规划，作图要细致认真，同时考查了向量的数量积，属于中档题．
练习册系列答案
相关题目
若函数f（x）=
x3+x2+mx是R上的单调函数，则实数m的取值范围是（ ）
| 1 |
| 3 |
| A、（1，+∞） |
| B、（-∞，1） |
| C、[1，+∞） |
| D、（-∞，1] |
若实数x，y满足不等式组
，则z=|x|+2y的最大值是（ ）
|
| A、10 | B、11 | C、13 | D、14 |
若函数f（x）=
ax3+
ax2-a+1的图象经过四个象限，则实数a的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、
| ||
B、a＜1或a＞
| ||
C、a＞-
| ||
D、1＜a＜
|