题目内容
若函数f（x）=
x3+x2+mx是R上的单调函数，则实数m的取值范围是（ ）
| 1 |
| 3 |
| A、（1，+∞） |
| B、（-∞，1） |
| C、[1，+∞） |
| D、（-∞，1] |
考点：利用导数研究函数的单调性
专题：函数的性质及应用
分析：先求函数f（x）的导数，然后根据f'（x）≥0或f′（x）≤0在R上恒成立，即可得到答案．
解答：
解：∵f'（x）=x2+2x+m，∴导函数为抛物线，开口向上，
∵要使f（x）在R上单调，
∴f'（x）=x2+2x+m≥0在R上恒成立，即m≥-x2-2x在R上恒成立，
∴m大于等于-x2-2x的最大值即可，
∵-x2-2x=-（x+1）2+1≤1，
∴m≥1
故选：C．
∵要使f（x）在R上单调，
∴f'（x）=x2+2x+m≥0在R上恒成立，即m≥-x2-2x在R上恒成立，
∴m大于等于-x2-2x的最大值即可，
∵-x2-2x=-（x+1）2+1≤1，
∴m≥1
故选：C．
点评：本题主要考查利用导数研究函数的单调性，要正确把握导数的正负与函数单调性之间的关系．
练习册系列答案
相关题目
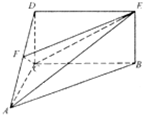如图，四边形BCDE为矩形，平面ABC⊥平面BCDE，AC⊥BC，AC=CD=