题目内容
已知数列{an}的前n项和Sn=
(n=1,2,3,…)
(1)求a1的值;
(2)求证:(n-2)an+1=(n-1)an-1(n≥2);
(3)判断数列{an}是否为等差数列,并说明理由.
| n(1+an) |
| 2 |
(1)求a1的值;
(2)求证:(n-2)an+1=(n-1)an-1(n≥2);
(3)判断数列{an}是否为等差数列,并说明理由.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)直接在数列递推式中取n=1求解a1的值;
(2)在数列递推式中取n=n-1得另一递推式,和原递推式作差后整理即可证得(n-2)an+1=(n-1)an-1(n≥2);
(3)数列{an}是等差数列,再在原递推式中取n=n-2得递推式,与n=n-1时的递推式作差,然后借助于等差中项的概念得答案.
(2)在数列递推式中取n=n-1得另一递推式,和原递推式作差后整理即可证得(n-2)an+1=(n-1)an-1(n≥2);
(3)数列{an}是等差数列,再在原递推式中取n=n-2得递推式,与n=n-1时的递推式作差,然后借助于等差中项的概念得答案.
解答:
(1)解:由Sn=
,得a1=S1=
,解得a1=1;
(2)证明:∵Sn=
,
∴Sn-1=
(n≥2).
两式作差得:an=
,
即(n-2)an+1=(n-1)an-1(n≥2);
(3)数列{an}是等差数列.
事实上,
由Sn=
,
∴Sn-1=
(n≥2).
Sn-2=
(n≥3).
由(2)可得,an-1=Sn-1-Sn-2=
(n≥3).
∴an-an-1=
.
即(n-2)an-2(n-2)an-1+(n-2)an-2=0.
∵n≥3,
∴an-2an-1+an-2=0,即an-an-1=an-1-an-2(n≥3).
∴数列{an}是以1为首项,a2-1为公差的等差数列.
| n(1+an) |
| 2 |
| 1+a1 |
| 2 |
(2)证明:∵Sn=
| n(1+an) |
| 2 |
∴Sn-1=
| (n-1)(1+an-1) |
| 2 |
两式作差得:an=
| nan+1-(n-1)an-1 |
| 2 |
即(n-2)an+1=(n-1)an-1(n≥2);
(3)数列{an}是等差数列.
事实上,
由Sn=
| n(1+an) |
| 2 |
∴Sn-1=
| (n-1)(1+an-1) |
| 2 |
Sn-2=
| (n-2)(1+an-2) |
| 2 |
由(2)可得,an-1=Sn-1-Sn-2=
| (n-1)an-1+1-(n-2)an-2 |
| 2 |
∴an-an-1=
| nan-2(n-1)an-1+(n-2)an-2 |
| 2 |
即(n-2)an-2(n-2)an-1+(n-2)an-2=0.
∵n≥3,
∴an-2an-1+an-2=0,即an-an-1=an-1-an-2(n≥3).
∴数列{an}是以1为首项,a2-1为公差的等差数列.
点评:本题考查了数列递推式,考查了等差关系的确定,考查了学生的计算能力,是中档题.

练习册系列答案
相关题目
设z=x+y,其中实数x,y满足
若z的最大值为12,则z的最小值为( )
|
| A、-3 | B、3 | C、-6 | D、6 |
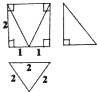
某几何体的三视图如图所示,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,在△ABC中,D为BC边上的一点,且BD=2DC.若
如图所示,在△ABC中,D为BC边上的一点,且BD=2DC.若 已知函数f(x)=x2+(2a-1)x-3,x∈[-2,3].
已知函数f(x)=x2+(2a-1)x-3,x∈[-2,3].