题目内容
已知数列{an}的前n项和Sn=
,n∈N*,
(1)求数列{an}的通项公式
(2)设bn=2an+an,求数列{ bn}的前n项的和.
| n2+n |
| 2 |
(1)求数列{an}的通项公式
(2)设bn=2an+an,求数列{ bn}的前n项的和.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用公式即可求得数列的通项公式;
(2)分组后利用等差数列、等比数列的求和公式求和即可.
(2)分组后利用等差数列、等比数列的求和公式求和即可.
解答:
解:(1)∵Sn=
,n∈N*,
∴当n=1时,a1=s1=1,
当n≥2时,an=sn-sn-1=
-
=n,
经检验对n=1也成立,
∴an=n(n∈N*).
(2)bn=2an+an=2n+n,
设数列{ bn}的前n项的和为Tn,
∴Tn=(2+22+…+2n)+(1+2+3+…+n)=
+
=2n+1+
-2.
| n2+n |
| 2 |
∴当n=1时,a1=s1=1,
当n≥2时,an=sn-sn-1=
| n2+n |
| 2 |
| (n-1)2+(n-1) |
| 2 |
经检验对n=1也成立,
∴an=n(n∈N*).
(2)bn=2an+an=2n+n,
设数列{ bn}的前n项的和为Tn,
∴Tn=(2+22+…+2n)+(1+2+3+…+n)=
| 2(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
点评:本题主要考查数列通项公式及前n项和的求法,考查等差数列、等比数列的求和公式及学生的运算求解能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知双曲线
-y2=1(a>0)的实轴长2,则该双曲线的离心率为( )
| x2 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以下说法正确的是( )
| A、若直线a不平行于平面α,则直线a与平面α相交 |
| B、直线a和b是异面直线,若直线c∥a,则c与b一定相交 |
| C、若直线a和b都和平面α平行,则a和b也平行 |
| D、若直线c平行直线a,直线b⊥a,则b⊥c |
设z=x+y,其中实数x,y满足
若z的最大值为12,则z的最小值为( )
|
| A、-3 | B、3 | C、-6 | D、6 |
若任取x,y∈[0,1],则点P(x,y)满足y>
的概率为( )
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
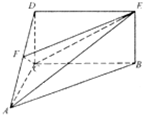 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=