Question

A，B，C是平面内不共线的三点，点P在该平面内且有，

PA

+2

PB

+3

PC

=

0

现将一粒黄豆随机撒在△ABC内，则这粒黄豆落在△PBC内的概率为

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：由已知得

AP

=

1

3

AB

+

1

2

AC

，设C到AB距离d，求出△PBC的面积，利用几何概型的概率公式解答．

解答： 解：由

PA

+2

PB

+3

PC

=

0

⇒-

AP

+2(

AB

-

AP

)+3(

AC

-

AP

)=

0

，
得

AP

=

1

3

AB

+

1

2

AC

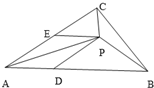
，设C到AB距离d，如图，
则S△PCE=

1

2

×

1

3

×AB×

1

2

d=

1

6

S△ABC，
S四边形ABPE=

1

2

(

1

3

AB+AB)×

1

2

d=

1

3

AB×d=

2

3

S△ABC，
所以S△PBC=(1-

1

6

-

2

3

)S△ABC=

1

6

S△ABC，所以所求概率为 

S△PBC

S△ABC

=

1

6

．
故答案为：

1

6

．

点评：本题考查了几何概型的概率求法；关键是求出满足条件的△PBC的面积，然后与△ABC的面积比为所求．