题目内容
已知函数f（x）=
&2sin
x，(|x|＜1|，则函数y=f（f（x））-1的零点个数是（ ）
|
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由题意作函数f（x）=
图象，由图象及复合函数的性质求解零点的个数．
|
解答：
解：作函数f（x）=
图象，如下，
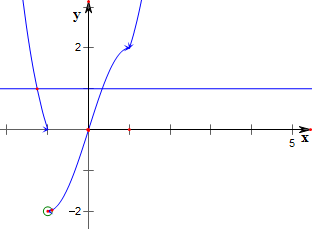
令y=f（f（x））-1=0，
则f（f（x））=1，由图知，
f（x）有两个值，一个值在（-2，-1）上，另一个值在（0，1）上，
由图知，f（x）在（-2，-1）上时有一个x值，
f（x）在（0，1）上时有两个x值，
故共有3个值，
故选C．
|
令y=f（f（x））-1=0，
则f（f（x））=1，由图知，
f（x）有两个值，一个值在（-2，-1）上，另一个值在（0，1）上，
由图知，f（x）在（-2，-1）上时有一个x值，
f（x）在（0，1）上时有两个x值，
故共有3个值，
故选C．
点评：本题考查了复合函数的应用及函数的零点的应用，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙两名同学至少有一人参加，那么不同的发言顺序的种数为（ ）
| A、840 | B、720 |
| C、600 | D、30 |