题目内容
已知抛物线C的顶点在坐标原点，焦点与双曲线：
-
=1的右焦点重合，则抛物线C的方程是 ．
| x2 |
| 7 |
| y2 |
| 2 |
考点：抛物线的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出双曲线的右焦点，设出抛物线的方程，由方程
=3，解得p，即可得到所求方程．
| p |
| 2 |
解答：
解：双曲线：
-
=1的右焦点为（3，0），
则设抛物线方程为y2=2px（p＞0），
由
=3，可得，p=6．
则抛物线方程为y2=12x．
故答案为：y2=12x．
| x2 |
| 7 |
| y2 |
| 2 |
则设抛物线方程为y2=2px（p＞0），
由
| p |
| 2 |
则抛物线方程为y2=12x．
故答案为：y2=12x．
点评：本题考查双曲线和抛物线的方程和性质，考查运算能力，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
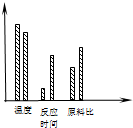如图，是某正交试验设计中绘制的产量和因素的关系图，由此图可知（ ）| A、影响试验结果最主要的因素是温度 |
| B、影响试验结果最主要的因素是反应时间 |
| C、影响试验结果最主要的因素是原料比 |
| D、因图中数据不全，无法分清哪个因素影响最大 |
已知曲线C：
-y2=1的左右焦点分别为F1F2，过点F2的直线与双曲线C的右支相交于P，Q两点，且点P的横坐标为2，则PF1Q的周长为（ ）
| x2 |
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、4
|
某数列第一项为1，并且对所有n≥2，n∈N*，数列的前n项之积n2，则当n≥2时，有（ ）
| A、an=2n-1 | ||
| B、an=n2 | ||
C、an=
| ||
D、an=
|
由曲线y=x2，y=
围成的封闭图形的面积为（ ）
| x |
A、
| ||
B、
| ||
C、
| ||
| D、1 |