题目内容
f(x)=ax(x-1)(a≠0)图象的顶点在函数y=log2x的图象上,若h(x)=|f(x)|+m恰有2个零点,求m的取值范围.
考点:对数函数的图像与性质,函数零点的判定定理
专题:函数的性质及应用
分析:由f(x)=ax(x-1)(a≠0)图象的顶点(
,-
),在函数y=log2x的图象上,可求出a值,进而得到f(x)的解析式,由函数图象的对折变换得到函数y=|f(x)|的图象,再由h(x)=|f(x)|+m恰有2个零点,则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,数形结合得到m的取值范围.
| 1 |
| 2 |
| a |
| 4 |
解答:
解:f(x)=ax(x-1)(a≠0)图象的顶点为(
,-
),
故-
=log2
=-1,故a=4,
故f(x)=4x(x-1),
则函数y=|f(x)|的图象如下图所示:
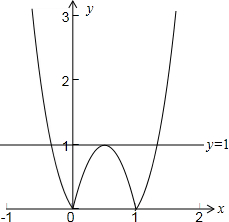
若h(x)=|f(x)|+m恰有2个零点,
则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,
故-m>1,或-m=0,
则m<-1或m=0.
| 1 |
| 2 |
| a |
| 4 |
故-
| a |
| 4 |
| 1 |
| 2 |
故f(x)=4x(x-1),
则函数y=|f(x)|的图象如下图所示:

若h(x)=|f(x)|+m恰有2个零点,
则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,
故-m>1,或-m=0,
则m<-1或m=0.
点评:本题考查的知识点是二次函数的图象和性质,对数函数的图象和性质,函数图象的对折变换,函数的零点,是函数的综合应用,难度中档.

练习册系列答案
相关题目
a<0且-1<b<0是a+ab<0的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |