题目内容
已知函数f(x)ax2+bx+c(x∈R,a>0)的零点为x1,x2(x1<x2),函数f(x)的最小值为y0,且y0∈[x1,x2],则函数y=f[f(x)]的零点个数是( )
| A、2或3 | B、3或4 | C、3 | D、4 |
考点:函数零点的判定定理
专题:证明题,函数的性质及应用
分析:如图所示,由于函数f(x)=ax2+bx+c(a>0)的零点为x1,x2(x1<x2),可得△=b2-4ac>0.由f(f(x))=af2(x)+bf(x)+c=0,利用△>0,可得f(x)=x1或f(x)=x2.已知函数f(x)的最小值为y0,且y0∈[x1,x2),画出直线y=x2.y=x1.即可得出交点个数,进而得到函数零点的个数.
解答:
解:如图所示,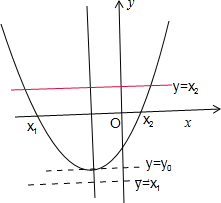
∵函数f(x)=ax2+bx+c(a>0)的零点为x1,x2(x1<x2),∴△=b2-4ac>0.
由f(f(x))=af2(x)+bf(x)+c=0,∵△>0,
∴f(x)=x1或f(x)=x2.
∵函数f(x)的最小值为y0,且y0∈[x1,x2),画出直线y=x2.y=x1.
则直线y=x2.与y=f(x)必有两个交点,此时f(x)=x2.有2个实数根,即函数y=f(f(x))由两个零点.
直线y=x1与y=f(x)可能有一个交点或无交点,此时f(x)=x1有一个实数根x=-
或无实数根.
综上可知:函数y=f(f(x))的零点由2个或3个.
故选:A

∵函数f(x)=ax2+bx+c(a>0)的零点为x1,x2(x1<x2),∴△=b2-4ac>0.
由f(f(x))=af2(x)+bf(x)+c=0,∵△>0,
∴f(x)=x1或f(x)=x2.
∵函数f(x)的最小值为y0,且y0∈[x1,x2),画出直线y=x2.y=x1.
则直线y=x2.与y=f(x)必有两个交点,此时f(x)=x2.有2个实数根,即函数y=f(f(x))由两个零点.
直线y=x1与y=f(x)可能有一个交点或无交点,此时f(x)=x1有一个实数根x=-
| b |
| 2a |
综上可知:函数y=f(f(x))的零点由2个或3个.
故选:A
点评:本题考查了二次函数的图象与性质、函数零点与图象交点的个数之间的关系等基础知识与基本技能方法,属于难题

练习册系列答案
相关题目