题目内容
令f(x)=2sinx+1,若集合A={x|
≤x≤
},B={x|-2+m<f(x)<2+m},若A?B,求实数m的取值范围.
| π |
| 6 |
| 2π |
| 3 |
考点:集合的包含关系判断及应用
专题:不等式的解法及应用,集合
分析:求出函数的值域,根据A?B,从而可得不等式组,解不等式,即可求出实数m的取值范围.
解答:
解∵
≤x≤
,
∴
≤sinx≤1,
∴2≤f(x)≤3,
∵A?B,m-2<f(x)<m+2,
∴
,
∴1<m<4.
| π |
| 6 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
∴2≤f(x)≤3,
∵A?B,m-2<f(x)<m+2,
∴
|
∴1<m<4.
点评:本题考查三角函数的性质,考查函数的值域,考查集合知识,考查学生分析解决问题的能力,正确运用正弦函数的单调性是关键.

练习册系列答案
相关题目
方程
=|x+y+2|表示( )
| 2(x+1)2+2(y-1)2 |
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
函数f(x)=lgx-
的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
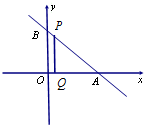 如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.
如图直线l过点(3,4),与x轴、y轴的正半轴分别交于A、B两点,△ABC的面积为24.点P为线段AB上一动点,且PQ∥QB交OA于点Q.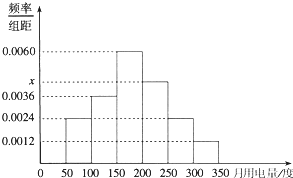 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求