Question

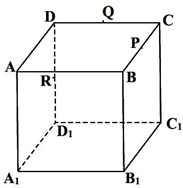如图，正方体ABCD-A₁B₁C₁D₁的棱长为2，P，Q，R分别是棱BC，CD，DD₁的中点．下列命题：
①过A₁C₁且与CD₁平行的平面有且只有一个；
②平面PQR截正方体所得截面图形是等腰梯形；
③AC₁与QR所成的角为60°；
④线段MN与GH分别在棱A₁B₁和CC₁上运动，则三棱锥M-NGH体积是定值；
⑤线段MN是该正方体内切球的一条直径，点O在正方体表面上运动，则

OM

•

ON

的最大值是2．
其中真命题的序号是

 

 （写出所有真命题的序号）．

Answer 1

考点：命题的真假判断与应用

专题：综合题,空间位置关系与距离

分析：①，利用线面平行的性质，过A₁C₁且与CD₁平行的平面为A₁BC₁，可判断①
②，作图可知，平面PQR截正方体所得截面图形是正六边形，可判断②；
③，利用三垂线定理可知，QR⊥AC₁，可判断③；
④，作图，可知V_M-NGH=V_G-MNH=VG-MNC1-VH-MNC1=

1

3

×2MN•GH，由于MN•GH不是定值，可判断④；
⑤，利用向量数量积的概念及性质，可知当点O，M，N三点共线时，

OM

•

ON

的取得最大值，继而可求得该最大值，可判断⑤．

解答： 解：对于①，∵CD₁∥A₁B，A₁B∩A₁C₁=A₁，
∴过A₁C₁且与CD₁平行的平面为A₁BC₁，有且只有一个，故①正确；
对于②，如图，平面PQR截正方体所得截面图形是正六边形，不是等腰梯形，故②错误；

对于③，∵QR∥CD₁，而CD₁

∥

.

A₁B，又AC₁在平面AA₁B₁B中的射影为AB₁，A₁B⊥AB₁，
由三垂线定理可知，A₁B⊥AC₁，即QR⊥AC₁，故③错误；
对于④，如图，

由图可知，V_M-NGH=V_G-MNH=VG-MNC1-VH-MNC1=

1

3

×2MN•GH，由于MN•GH不是定值，故④错误；
对于⑤，设点P为此正方体的内切球的球心，半径R=1．
∵

OM

•

ON

≤|

OM

|•|

ON

|，∴当点O，M，N三点共线时，

OM

•

ON

的取得最大值．
此时，

OM

•

ON

≤（|

OP

|+|

PM

|）•（|

OP

|-|

PN

|），而|

PM

|=|

PN

|=1，
∴

OM

•

ON

≤|PO|²-1，当且仅当点P为正方体的一个顶点时上式取得最大值，又正方体的对角线长为2

3

，
∴(

OM

•

ON

)max=(

2 3

2

)2-1=2，
故答案为：①⑤．

点评：本题考查空间线面、面面之间的位置关系，考查作图能力、推理运算能力，考查平面向量的数量积的概念及性质的应用，属于难题．