题目内容
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知向量$\overrightarrow{m}$=((b+c)2,-1),$\overrightarrow{n}$=(1,a2+bc),且$\overrightarrow{m}$•$\overrightarrow{n}$=0.(1)求角A的大小;
(2)若a=3,求△ABC的周长的取值范围.
分析 (1)根据平面向量的数量积,利用余弦定理,即可求出角A的大小;
(2)利用余弦定理和基本不等式,求出b+c的取值范围,再根据三角形三边关系,即可求出△ABC周长的取值范围.
解答 解:(1)向量$\overrightarrow{m}$=((b+c)2,-1),$\overrightarrow{n}$=(1,a2+bc),
∴$\overrightarrow{m}$•$\overrightarrow{n}$=(b+c)2-(a2+bc)=0,
∴b2+c2-a2=-bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=-$\frac{bc}{2bc}$=-$\frac{1}{2}$;
又A∈(0,π),
∴A=$\frac{2π}{3}$;
(2)由a=3,结合余弦定理得
a2=b2+c2+bc
=(b+c)2-bc≥(b+c)2-${(\frac{b+c}{2})}^{2}$
=$\frac{3}{4}$(b+c)2,
∴(b+c)2≤12,
∴b+c≤2$\sqrt{3}$,
∴a+b+c≤3+2$\sqrt{3}$,
∴6<a+b+c≤3+2$\sqrt{3}$,
∴△ABC的周长的取值范围是(6,3+2$\sqrt{3}$].
点评 本题考查了平面向量的数量积和余弦定理、基本不等式以及三角形三边关系的应用问题,是综合题.

练习册系列答案
相关题目
20.复数z=2-i在复平面对应的点在第几象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.按如图的规律所拼成的一图案共有1024个大小相同的小正三角形“△”或“?”,则该图案共有( )


| A. | 16层 | B. | 32层 | C. | 64层 | D. | 128层 |
4.如图,网格纸上小正方形的边长为1,粗线画出的是一个四棱锥的三视图,则该四棱锥最长棱的棱长为( )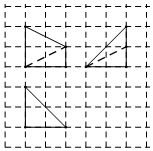

| A. | 3 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
5.若复数z满足($\sqrt{3}$-2i)z=6i(i是虚数单位),则z=( )
| A. | $\frac{-12+6\sqrt{3}i}{7}$ | B. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i |