题目内容
4.如图,网格纸上小正方形的边长为1,粗线画出的是一个四棱锥的三视图,则该四棱锥最长棱的棱长为( )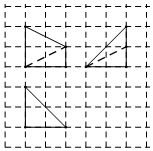
| A. | 3 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
分析 作出直观图,根据三视图的数据和勾股定理计算各棱长即可.
解答  解:作出四棱锥P-ABCD的直观图如图所示:
解:作出四棱锥P-ABCD的直观图如图所示:
由三视图可知底面ABCD是直角梯形,AD∥BC,AB⊥AD,
侧面PAB⊥底面ABCD,AP⊥AB,
且AB=AD=AP=2,BC=1,
∴PD=PB=2$\sqrt{2}$,PC=3,CD=$\sqrt{5}$,
∴PC为四棱锥的最长棱.
故选A.
点评 本题考查了棱锥的结构特征和三视图,属于中档题.

练习册系列答案
相关题目
16.某几何体的三视图如图所示,俯视图是半径为2的圆,则该几何体的表面积为( )

| A. | 24π | B. | 16π | C. | 12π | D. | 8π |
13.已知函数f(x)的定义域为R.当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>$\frac{1}{2}$时,f(x+$\frac{1}{2}$)=f(x-$\frac{1}{2}$).则f (8)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
14.已知集合A={x|0<x<5,x∈Z},B={y|y=3n-2,n∈A},则A∩B=( )
| A. | {1} | B. | {4} | C. | {1,3} | D. | {1,4} |
 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f'(x)的图象如图所示,且经过点(1,0),(2,0).
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f'(x)的图象如图所示,且经过点(1,0),(2,0).