题目内容
已知抛物线C:x2=2py(p>0)的焦点为F,且
=4
,其中O是坐标原点,以G为圆心且与抛物线C有且只有两个交点的圆的方程为( )
| OG |
| OF |
| A、x2+(y-2p)2=3p2 |
| B、(x-2p)2+y2=3p2 |
| C、x2+(y-2p)2=p2 |
| D、(x-2p)2+y2=p2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求出G的坐标,再设以G为圆心的圆的方程为x2+(y-2p)2=r2,将x2=2py代入,整理,根据以G为圆心且与抛物线C有且只有两个交点,可得△=4p2-4(4p2-r2)=0,由此可求圆的半径,即可得到结论.
解答:
解:∵抛物线C:x2=2py(p>0)的焦点为F,且
=4
,
∴G(0,2p),
设以G为圆心的圆的方程为x2+(y-2p)2=r2,
将x2=2py代入,整理可得y2-2py+4p2-r2=0
∵以G为圆心且与抛物线C有且只有两个交点,
∴△=4p2-4(4p2-r2)=0,
∴r2=3p2,
∴以G为圆心的圆的方程为x2+(y-2p)2=3p2.
故选:A.
| OG |
| OF |
∴G(0,2p),
设以G为圆心的圆的方程为x2+(y-2p)2=r2,
将x2=2py代入,整理可得y2-2py+4p2-r2=0
∵以G为圆心且与抛物线C有且只有两个交点,
∴△=4p2-4(4p2-r2)=0,
∴r2=3p2,
∴以G为圆心的圆的方程为x2+(y-2p)2=3p2.
故选:A.
点评:本题考查圆的方程,考查圆与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
正四面体ABCD,线段AB∥平面α,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面α上的射影所成角余弦值的范围是( )
A、[0,
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
已知α为第二象限角,且sinα=
,则tanα的值为( )
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在空间中有一棱长为a的正四面体,其俯视图的面积的最大值为( )
| A、a2 | ||||
B、
| ||||
C、
| ||||
D、
|
将函数h(x)=2sin(2x+
)的图象向右平移
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象与函数h(x)的图象( )
| π |
| 4 |
| π |
| 4 |
| A、关于直线x=0对称 |
| B、关于直线x=1对称 |
| C、关于点(1,0)对称 |
| D、关于点(0,1)对称 |
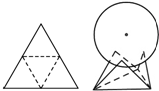 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为
用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为