题目内容

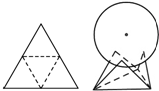用一个边长为4的正三角形硬纸，沿各边中点连线垂直折起三个小三角形，做成一个蛋托，半径为1的鸡蛋（视为球体）放在其上（如图），则鸡蛋中心（球心）与蛋托底面的距离为
 
．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：画出图形，判断蛋槽的底面三角形的形状，求出蛋槽的高，判断球心与蛋槽的上底面三棱锥的形状，然后求出棱锥的高即可．
解答： 解：由题意可知折叠后的蛋槽的上顶点在底面的射影如图中红线三角形，
蛋槽的底面是正三角形边长为2，∴蛋槽的高为
3
，
且折起三个小三角形顶点构成边长为1的等边三角形A′B′C′，
O-A′B′C′是列出为1的正四面体，
∴球心到面A′B′C′的距离d=
1-(
3
3
)2
=
6
3
，
∴鸡蛋中心与蛋巢底面的距离为
3
+
6
3
．
故答案为：
3
+
6
3
．
点评：本题考查空间想象能力，逻辑推理能力，点到平面距离的求法，考查计算能力．
练习册系列答案
相关题目
已知△EFG中，点E（-1，2），点F（-2，-3），点G（1，1），求EG边上的高．
（Ⅰ）已知函数：f（x）=2n-1（xn+a）-（x+a）n，（x∈[0，+∞），n∈N*）求函数f（x）的最小值；
（Ⅱ）证明：
a n+b n
2
≥（
a+b
2
）n（a＞0，b＞0，n∈N*）；
（Ⅲ）定理：若a1，a2，a3，ak均为正数，则有
a
n
1
+a
n
2
+a
n
3
+…
+a
n
k
k
≥（
a1+a2+a3+…ak
k
）n成立（其中k≥2，k∈N*，k为常数．请你构造一个函数g（x），证明：当a1，a2，a3，…ak，ak+1均为正数时，
a
n
1
+a
n
2
+a
n
3
+
…a
n
k+1
k+1
≥（
a1+a2+a3+…ak+1
k+1
）n．
等比数列{an}中，若a3a5a7a9=16，则a5a7=
 
．
在三棱柱ABC-A1B1C1中侧棱垂直于底面，∠ACB=90°，∠BAC=30°，BC=1，且三棱柱ABC-A1B1C1的体积为3，则三棱柱ABC-A1B1C1的外接球的表面积为
 
．
直线l：
x=tcosα
y=1+tsinα
（t为参数）与圆C：
x=2+8cosθ
y=1+8sinθ
（θ为参数）相交所得的弦长的取值范围是
 
．
已知3sin2α+2sin2β=1，3（sinα+cosα）2-2（sinβ+cosβ）2=1，则cos2（α+β）=
 
．
若f（cosθ）=sin2θ-3sinθ，则f（2cos
π
3
）=
 
．
已知抛物线C：x2=2py（p＞0）的焦点为F，且
OG
=4
OF
，其中O是坐标原点，以G为圆心且与抛物线C有且只有两个交点的圆的方程为（　　）
A、x2+（y-2p）2=3p2
B、（x-2p）2+y2=3p2
C、x2+（y-2p）2=p2
D、（x-2p）2+y2=p2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网