题目内容
正四面体ABCD,线段AB∥平面α,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面α上的射影所成角余弦值的范围是( )
A、[0,
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
考点:异面直线及其所成的角
专题:空间角
分析:取AC中点为G,由已知条件推导出线段AB、EF在平面α上的射影所成角等于GF与EF在平面α上的射影所成角,当CD与平面α垂直时,EF在平面α上的射影E1F1的长取得最小值
,当CD与平面α平行时,E1F1取得最大值
,由此能求出AB与EF在平面α上的射影所成角余弦值的范围.
| 1 |
| 2 |
| ||
| 2 |
解答:
解:如图,取AC中点为G,
∵E,F分别是线段AD和BC的中点,∴GF∥AB,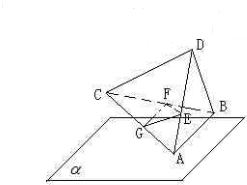
∴线段AB、EF在平面α上的射影所成角等于GF与EF在平面α上的射影所成角,
在正四面体中,AB⊥CD,又GE∥CD,
∴GE⊥GF,∴EF2=GE2+GF2,
当四面体绕AB转动时,∵GF∥平面α,GE与GF的垂直性保持不变,
∴当CD与平面α垂直时,GE在平面上的射影长最短为0,
此时EF在平面α上的射影E1F1的长取得最小值
,
当CD与平面α平行时,GE在平面上的射影长最长为
,E1F1取得最大值
,
∴射影E1F1长的取值范围是[
,
],
而GF在平面α上的射影长为定值
,
∴AB与EF在平面α上的射影所成角余弦值的范围是[
,1].
故选:B.
∵E,F分别是线段AD和BC的中点,∴GF∥AB,

∴线段AB、EF在平面α上的射影所成角等于GF与EF在平面α上的射影所成角,
在正四面体中,AB⊥CD,又GE∥CD,
∴GE⊥GF,∴EF2=GE2+GF2,
当四面体绕AB转动时,∵GF∥平面α,GE与GF的垂直性保持不变,
∴当CD与平面α垂直时,GE在平面上的射影长最短为0,
此时EF在平面α上的射影E1F1的长取得最小值
| 1 |
| 2 |
当CD与平面α平行时,GE在平面上的射影长最长为
| 1 |
| 2 |
| ||
| 2 |
∴射影E1F1长的取值范围是[
| 1 |
| 2 |
| ||
| 2 |
而GF在平面α上的射影长为定值
| 1 |
| 2 |
∴AB与EF在平面α上的射影所成角余弦值的范围是[
| ||
| 2 |
故选:B.
点评:本题考查两条直线在平面上的射影所成角的余弦值的范围的求法,解题时要注意空间思维能力的培养,注意旋转问题的合理运用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
已知命题p:“直线l⊥平面α内的无数条直线”的充要条件是“l⊥α”,命题q:若平面α⊥平面β,直线a?β,则“a⊥α”是“a∥β”的充分不必要条件,则下列命题中正确的( )
| A、p∧q | B、p∨¬q |
| C、¬p∧¬q | D、¬p∧q |
已知抛物线C:x2=2py(p>0)的焦点为F,且
=4
,其中O是坐标原点,以G为圆心且与抛物线C有且只有两个交点的圆的方程为( )
| OG |
| OF |
| A、x2+(y-2p)2=3p2 |
| B、(x-2p)2+y2=3p2 |
| C、x2+(y-2p)2=p2 |
| D、(x-2p)2+y2=p2 |
已知x,y满足
,则
的取值范围是( )
|
| x+y-6 |
| x-4 |
A、[0,
| ||
B、[0,
| ||
C、[1,
| ||
D、[2,
|