��Ŀ����
5����֪����{an+1-2an}��n��N*���ǹ���Ϊ2�ĵȱ����У�����a1=1��a2=4������֤��������$\{\frac{a_n}{2^n}\}$�ǵȲ����У�
����������{an}��ǰn���Sn��
�� III��������${c_n}=\frac{{2{a_n}-2n}}{n}����n��2��$��֤����$\frac{1}{2}-{��\frac{1}{2}��^n}��\frac{1}{c_2}+\frac{1}{c_3}+��+\frac{1}{c_n}��1-{��\frac{1}{2}��^{n-1}}$��
���� ����ͨ���ȱ����е�ͨ�ʽ��֪an+1-2an=2n������ͬ��2n+1���ý��ۣ�
�������ô�λ��������㼴�ý��ۣ�
�������÷���������֤����
��� �⣺����֤��������֪��${a_{n+1}}-2{a_n}=��{a_2}-2{a_1}��•{2^{n-1}}={2^n}$��
����ͬ��2n+1�ã�$\frac{{{a_{n+1}}}}{{{2^{n+1}}}}-\frac{a_n}{2^n}=\frac{1}{2}$��
��������$\{\frac{a_n}{2^n}\}$��������Ϊ$\frac{1}{2}$������Ϊ$\frac{1}{2}$�ĵȲ����У�
�����ɣ���֪$\frac{a_n}{2^n}=\frac{1}{2}n$������${a_n}=n•{2^{n-1}}$��
${S_n}=1•{2^0}+2•{2^1}+��+n•{2^{n-1}}$��
��2Sn=1•21+2•22+��+n•2n��
����ã�$-{S_n}=1•{2^0}+{2^1}+��+{2^{n-1}}-n•{2^n}$��
����$-{S_n}=\frac{{1-{2^n}}}{1-2}-n•{2^n}$��
��${S_n}=��n-1��{2^n}+1$��
����֤��������cn=2n-2��n��2��
��$\frac{1}{c_n}=\frac{1}{{{2^n}-2}}��\frac{1}{2^n}$��
��$\frac{1}{c_2}+\frac{1}{c_3}+��+\frac{1}{c_n}��\frac{1}{2^2}+\frac{1}{2^3}+��+\frac{1}{2^n}=\frac{{\frac{1}{4}[1-{{��\frac{1}{2}��}^{n-1}}]}}{{1-\frac{1}{2}}}=\frac{1}{2}-{��\frac{1}{2}��^n}$
�֡�$\frac{1}{c_n}=\frac{1}{{{2^n}-2}}��\frac{2}{2^n}={��\frac{1}{2}��^{n-1}}$����n��3����
��n=2ʱ��$\frac{1}{c_2}=\frac{1}{2}$��
��$\frac{1}{{c}_{2}}+\frac{1}{{c}_{3}}+��+\frac{1}{{c}_{n}}$��$\frac{1}{{2}^{1}}+\frac{1}{{2}^{2}}+��+\frac{1}{{2}^{n-1}}$=$\frac{\frac{1}{2}[1-��\frac{1}{2}��^{n-1}]}{1-\frac{1}{2}}$=1-��$\frac{1}{2}$��n-1��
����ԭ����ʽ��֤��
���� ���⿼�����е�ͨ�ǰn��Ͳ���ʽ��֤�����Ա���ʽ�������μ���λ������ͷ����ǽ������Ĺؼ���ע����ⷽ���Ļ��ۣ������е��⣮

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д� ��IJ�Ϸ��ǡ����ҹ��Ŵ���ѧ�������о��������Ĺ����й����һ����г�����ļ����壬������ȫ��ͬ���ĸ����湹�ɣ���Ե�����������ͬһԲ���IJ����ϣ����������ۺϣ�IJ�ϣ���һ��ķ���ɡ�����ǣ�����ͼ��������ABCD��Ϊ������ֱ���������ĸ����ߣ����ü����������ͼ�����ͼ���ǰ뾶Ϊr��Բ�������敜ԭ��������øü���������Ϊ��������
��IJ�Ϸ��ǡ����ҹ��Ŵ���ѧ�������о��������Ĺ����й����һ����г�����ļ����壬������ȫ��ͬ���ĸ����湹�ɣ���Ե�����������ͬһԲ���IJ����ϣ����������ۺϣ�IJ�ϣ���һ��ķ���ɡ�����ǣ�����ͼ��������ABCD��Ϊ������ֱ���������ĸ����ߣ����ü����������ͼ�����ͼ���ǰ뾶Ϊr��Բ�������敜ԭ��������øü���������Ϊ��������| A�� | $\frac{8}{3}{r^3}$ | B�� | $\frac{8}{3}��{r^3}$ | C�� | $\frac{16}{3}{r^3}$ | D�� | $\frac{16}{3}��{r^3}$ |
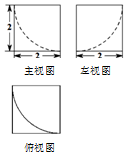
| A�� | $8-\frac{4}{3}��$ | B�� | $8-\frac{8}{3}��$ | C�� | 24-�� | D�� | 24+�� |
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | 1��$\frac{1}{2}$ | D�� | ��ȷ�� |
| A�� | 0 | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{2}$ |
| A�� | $\sqrt{3}$ | B�� | $\frac{{\sqrt{3}}}{3}$ | C�� | -$\frac{{\sqrt{3}}}{3}$ | D�� | -$\sqrt{3}$ |