题目内容
10.已知数列{an}中,a3=2,a7=1,若数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$是等差数列,则a11等于( )| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
分析 由已知结合等差数列的性质列式计算.
解答 解:∵数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$是等差数列,
∴$\frac{1}{1+{a}_{3}}+\frac{1}{1+{a}_{11}}=\frac{2}{1+{a}_{7}}$,
∵a3=2,a7=1,
∴$\frac{2}{1+1}=\frac{1}{1+2}+\frac{1}{1+{a}_{11}}$,解得${a}_{11}=\frac{1}{2}$.
故选:D.
点评 本题考查等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
1.复数z满足z=$\frac{7+i}{1-2i}$(i为虚数单位),则复数z的共轭复数$\overline{z}$=( )
| A. | 1+3i | B. | 1-3i | C. | 3-i | D. | 3+i |
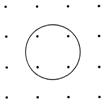 如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.
如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.