题目内容
13.已知函数f(x)=4x3+ax2+bx+5在x=-1与x=$\frac{3}{2}$处有极值,则函数的单调递减区间为(-1,$\frac{3}{2}$).分析 首先求出函数的导数,然后f′(-1)=0,f′( $\frac{3}{2}$)=0,解出a、b的值,求出函数的解析式;由f′(x)<0,求出函数的单调区间;求出函数的增区间,
解答 解:(Ⅰ)解:f′(x)=12x2+2ax+b,依题意有f′(-1)=0,f($\frac{3}{2}$ )=0,
即$\left\{\begin{array}{l}{12-2a+b=0}\\{27+3a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-3}\\{b=-18}\end{array}\right.$.
所以f(x)=4x3-3x2-18x+5
由f′(x)=12x2-6x-18<0,
∴(-1,$\frac{3}{2}$)是函数的减区间
故答案为:(-1,$\frac{3}{2}$).
点评 此题主要考查多项式函数的导数,函数单调性的判定,考查运算求解能力、推理论证能力及分析与解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.已知函数f(x)=$\left\{\begin{array}{l}{-x+1,x<1}\\{{2}^{x}-2,x≥1}\end{array}\right.$,g(x)=$\frac{1}{x}$,若对任意x∈[m,+∞)(m>0),总存在两个x0∈[0,2],使得f(x0)=g(x),则实数m的取值范围是( )
| A. | [1,+∞) | B. | (0,1] | C. | [$\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$] |
1.复数z满足z=$\frac{7+i}{1-2i}$(i为虚数单位),则复数z的共轭复数$\overline{z}$=( )
| A. | 1+3i | B. | 1-3i | C. | 3-i | D. | 3+i |
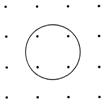 如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.
如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.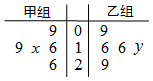 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )