题目内容
14.已知函数f(x)=(x2-a+1)ex,g(x)=(x2-2)ex+2(1)若函数f(x)在区间[-2,2]上是单调函数,求实数a的取值范围;
(2)若f(x)有两个不同的极值点m,n(m<n),且2(m+n)≤mn-1,记F(x)=e2f(x)+g(x),求F(m)的取值范围.
分析 (1)f′(x)=(x2+2x+1-a)ex,令u(x)=x2+2x+1-a=(x+1)2-a.u(-1)=-a,u(-2)=1-a,u(2)=9-a.由函数f(x)在区间[-2,2]上是单调函数,可得u(x)≤0,或u(x)≥0,x∈[-2,2].利用二次函数的单调性即可得出.
(2)f(x)有两个不同的极值点m,n(m<n),即u(x)=x2+2x+1-a=(x+1)2-a=0有两个不等的实数根m,n.可得-a<0,且m+n=-2,mn=1-a.再根据2(m+n)≤mn-1,可得0<a≤4.另一方面:m=-1-$\sqrt{a}$.F(x)=e2f(x)+g(x)=ex+2(2x2-a-1),F(m)=em+2(2m2-a-1)=${e}^{1-\sqrt{a}}$$(a+4\sqrt{a}+1)$,令$\sqrt{a}$=t∈(0,2].令h(t)=e1-t(t2+4t-1),t∈(0,2].利用导数研究其单调性极值与最值即可得出.
解答 解:(1)f′(x)=(x2+2x+1-a)ex,
令u(x)=x2+2x+1-a=(x+1)2-a.
u(-1)=-a,u(-2)=1-a,u(2)=9-a.
∵函数f(x)在区间[-2,2]上是单调函数,∴u(x)≤0,或u(x)≥0,x∈[-2,2].
∴9-a≤0,或-a≥0,
解得a≥9,或a≤0.
∴a≥9时,u(x)≤0,f′(x)≤0,函数f(x)在x∈[-2,2]上单调递减.
a≤0时,u(x)≥0,f′(x)≥0,函数f(x)在x∈[-2,2]上单调递增.
(2)∵f(x)有两个不同的极值点m,n(m<n),
∴u(x)=x2+2x+1-a=(x+1)2-a=0有两个不等的实数根m,n.
∴-a<0,解得a>0.
且m+n=-2,mn=1-a.
∵2(m+n)≤mn-1,
∴-4≤1-a-1,解得a≤4.
∴0<a≤4.
另一方面:m=-1-$\sqrt{a}$.
F(x)=e2f(x)+g(x)=e2•(x2-a+1)ex+(x2-2)ex+2=ex+2(2x2-a-1),
F(m)=em+2(2m2-a-1)=${e}^{1-\sqrt{a}}$$(a+4\sqrt{a}+1)$,令$\sqrt{a}$=t∈(0,2].
则h(t)=e1-t(t2+4t-1),t∈(0,2].
h′(t)=$\frac{-e({t}^{2}+2t-5)}{{e}^{t}}$=$\frac{-e[t+(1+\sqrt{6})][t-(\sqrt{6}-1)]}{{e}^{t}}$,
∴h(t)在(0,$\sqrt{6}$-1]上单调递增,在($\sqrt{6}$-1,2]上单调递减.
h(0)=-e,h(2)=$\frac{7}{e}$,$h(\sqrt{6}-1)$=2+2$\sqrt{6}$.
∴h(t)∈$(-e,2+2\sqrt{6}]$.
即F(m))∈$(-e,2+2\sqrt{6}]$.
点评 本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法,考查了推理能力与计算能力,属于难题.

| A. | [1,+∞) | B. | (0,1] | C. | [$\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$] |
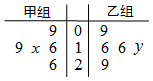 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
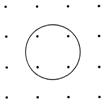 如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.
如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.