题目内容
如果实数x,y满足(x-3)2+(y-3)2=6.求:
(1)
的最大值与最小值;
(2)x+y的最大值与最小值;
(3)
的最大值与最小值.
(1)
| y |
| x |
(2)x+y的最大值与最小值;
(3)
| (x-2)2+y2 |
考点:圆方程的综合应用
专题:综合题,直线与圆
分析:(1)设k=
,则y=kx,由圆心(3,3)到直线的距离d=
=
,可得k=3±2
,即可求出)
的最大值与最小值;
(2)设x+y=m,即x+y-m=0,由圆心(3,3)到直线的距离d=
=
,可得m=6±2
,即可求出x+y的最大值与最小值;
(3)求出(2,0)与圆心(3,3)的距离,即可求出
的最大值与最小值.
| y |
| x |
| |3k-3| | ||
|
| 6 |
| 2 |
| y |
| x |
(2)设x+y=m,即x+y-m=0,由圆心(3,3)到直线的距离d=
| |6-m| | ||
|
| 6 |
| 3 |
(3)求出(2,0)与圆心(3,3)的距离,即可求出
| (x-2)2+y2 |
解答:
解:(1)设k=
,则y=kx,
由圆心(3,3)到直线的距离d=
=
,可得k=3±2
,
∴
的最大值与最小值分别为3+2
;3-2
;
(2)设x+y=m,即x+y-m=0,
由圆心(3,3)到直线的距离d=
=
,可得m=6±2
,
∴x+y的最大值与最小值分别为6+2
;6-2
;
(2)(2,0)与圆心(3,3)的距离为
=
,
∴
的最大值与最小值分别为
+
;
-
.
| y |
| x |
由圆心(3,3)到直线的距离d=
| |3k-3| | ||
|
| 6 |
| 2 |
∴
| y |
| x |
| 2 |
| 2 |
(2)设x+y=m,即x+y-m=0,
由圆心(3,3)到直线的距离d=
| |6-m| | ||
|
| 6 |
| 3 |
∴x+y的最大值与最小值分别为6+2
| 3 |
| 3 |
(2)(2,0)与圆心(3,3)的距离为
| 1+9 |
| 10 |
∴
| (x-2)2+y2 |
| 10 |
| 6 |
| 10 |
| 6 |
点评:本题考查圆方程的综合应用,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
命题P:函数f(x)=(
)x-sinx至少有两个零点,对于命题P的否定,下列说法正确的是( )
| 1 |
| 3 |
A、命题P的否定:函数f(x)=(
| ||
B、命题P的否定:函数f(x)=(
| ||
C、命题P的否定:函数f(x)=(
| ||
D、命题P的否定:函数f(x)=(
|
 地球北纬45°圈上有A、B两点,点A在东经30°处,点B在东经120°处,如图,若地球半径为R,则A、B两点在纬度圈上的劣弧长为( )
地球北纬45°圈上有A、B两点,点A在东经30°处,点B在东经120°处,如图,若地球半径为R,则A、B两点在纬度圈上的劣弧长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
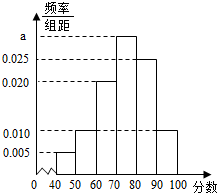 从某校高三年级学生中抽取40名学生,将他们高中学业水平考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
从某校高三年级学生中抽取40名学生,将他们高中学业水平考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.