题目内容
8.如图所示,从左到右依次为:一个长方体截去一个角所得多面体的直观图,该多面体的正视图,该多面体的侧视图(单位:cm)(1)按照给出的尺寸,求该多面体的体积;
(2)在所给直观图中连结BC′,证明:BC′∥平面EFG.
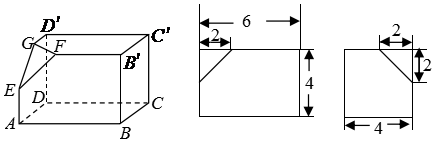
分析 (1)所求多面体体积V=V长方体-V正三棱锥’
(2)证明EG∥BC′即可.
解答 解析:(1)所求多面体体积V=V长方体-V正三棱锥=4×4×6-$\frac{1}{3}×(\frac{1}{2}×2×2)×2$=$\frac{284}{3}(c{m^3})$
(2)证明:在长方体ABCD-A′B′C′D′中,
连结AD′,则AD′∥BC′.因为E,G分别
为AA′,A′D′中点,所以AD′∥EG,
从而EG∥BC′.又BC′?平面EFG,所以BC′∥面EFG.
点评 本题考查了空间线面平行的判定,即体积公式的应用.属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{DC}$=(-1,3,0),则异面直线AB与DC所成角θ的大小为( )
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
19.已知集合A={x|(3-x)(x+1)>0},B={x|-2<x≤1},则A∩B=( )
| A. | (-1,1] | B. | (-2,3] | C. | (-2,-1) | D. | (-2,1-)∪[1,3) |
16.已知幂函数$f(x)={(m-1)^2}{x^{{m^2}-4m+2}}$在(0,+∞)上单调递增,函数g(x)=2x-t,?x1∈[1,6)时,总存在x2∈[1,6)使得f(x1)=g(x2),则t的取值范围是( )
| A. | ∅ | B. | t≥28或t≤1 | C. | t>28或t<1 | D. | 1≤t≤28 |
13.p:x>1,q:x>0,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{A{A_1}}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{BM}$可表示为( )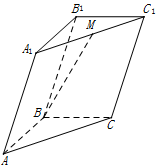

| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
18.将3本相同的语文书和2本相同的数学书分给四名同学,每人至少1本,不同的分配方法数有( )
| A. | 24 | B. | 28 | C. | 32 | D. | 36 |
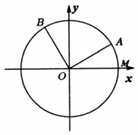 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.