题目内容

19．已知集合A={x|（3-x）（x+1）＞0}，B={x|-2＜x≤1}，则A∩B=（　　）
A．（-1，1]B．（-2，3]C．（-2，-1）D．（-2，1-）∪[1，3）

分析 求出A中不等式的解集，找出A与B的交集即可．

解答 解：由A中不等式变形得：（x-3）（x+1）＜0，
解得：-1＜x＜3，即A=（-1，3），
∵B={x|-2＜x≤1}=（-2，1]，
则A∩B=（-1，1]，
故选：A．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
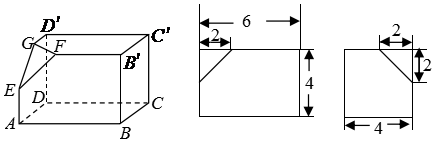
9．某几何体的三视图如图所示，则该几何体的表面积是（　　）
A．$\frac{\sqrt{2}}{3}$πB．2$\sqrt{2}$+2πC．$\frac{2\sqrt{2}}{3}$πD．2$\sqrt{2}$+$\frac{3}{2}$π
10．在平面直角坐标系xOy中，若双曲线${x^2}-\frac{y^2}{b^2}=1（b＞0）$的焦点到其渐近线的距离等于抛物线y2=2px上的点M（1，2）到其焦点的距离，则实数b=2．
7．已知A={x|x+1＞0}，B={-2，-1，0，1}，则（∁RA）∩B=（　　）
A．A={0，1，2}B．{-2}C．{-1，0，1}D．{-2，-1}
14．若实数k满足0＜k＜9，则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的（　　）
A．离心率相等B．虚半轴长相等C．实半轴长相等D．焦距相等
4．函数f（x）=3sin（2x-$\frac{π}{3}$）的图象为C，如下结论中正确的是①②③．
①图象C关于直线x=$\frac{11}{12}$π对称；      
②函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{12}$）内是增函数；
③图象C关于点（$\frac{2π}{3}$，0）对称；   
④由y=3sin2x图象向右平移$\frac{π}{3}$个单位可以得到图象C．
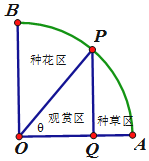11．如图，一个圆心角为直角的扇形AOB 花草房，半径为1，点P 是花草房弧上一个动点，不含端点，现打算在扇形BOP 内种花，PQ⊥OA，垂足为Q，PQ 将扇形AOP
分成左右两部分，在PQ 左侧部分三角形POQ 为观赏区，在PQ 右侧部分种草，已知种花的单位面积的造价为3a，种草的单位面积的造价为2a，其中a 为正常数，设∠AOP=θ，种花的造价与种草的造价的和称为总造价，不计观赏区的造价，设总造价为f（θ）
（1）求f（θ）关于θ 的函数关系式；
（2）求当θ 为何值时，总造价最小，并求出最小值．
8．如图所示，从左到右依次为：一个长方体截去一个角所得多面体的直观图，该多面体的正视图，该多面体的侧视图（单位：cm）
（1）按照给出的尺寸，求该多面体的体积；
（2）在所给直观图中连结BC′，证明：BC′∥平面EFG．
9．已知圆C经过A（-2，1），B（5，0）两点，且圆心C在直线y=2x上．
（1）求圆C的标准方程；
（2）设动直线l：（m+2）x+（2m+1）y-7m-8=0与圆C相交于P，Q两点，求|PQ|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网