题目内容
18.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{DC}$=(-1,3,0),则异面直线AB与DC所成角θ的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
分析 根据条件便可求出$|\overrightarrow{AB}|,|\overrightarrow{DC}|$,以及$\overrightarrow{AB}•\overrightarrow{DC}$的值,从而可求出$cos<\overrightarrow{AB},\overrightarrow{DC}>$的值,进而得出异面直线AB与DC所成角θ的大小.
解答 解:$|\overrightarrow{AB}|=\sqrt{20}=2\sqrt{5}$,$|\overrightarrow{DC}|=\sqrt{10}$,$\overrightarrow{AB}•\overrightarrow{DC}=10$;
∴$cos<\overrightarrow{AB},\overrightarrow{DC}>=\frac{10}{2\sqrt{5}×\sqrt{10}}=\frac{\sqrt{2}}{2}$;
∴$<\overrightarrow{AB},\overrightarrow{DC}>=45°$;
∴异面直线AB与DC所成角θ的大小为45°.
故选A.
点评 考查根据向量坐标求向量长度的公式,向量数量积的坐标运算,以及向量夹角余弦的坐标公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.某几何体的三视图如图所示,则该几何体的表面积是( )
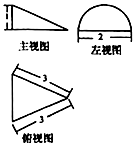

| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
13.已知幂函数f(x)的图象过点$(2,\frac{{\sqrt{2}}}{2})$,则f(x)是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
3.已知函数f(x)=|x|,则下列结论正确的是( )
| A. | 奇函数,在(-∞,0)上是减函数 | B. | 奇函数,在(-∞,0)上是增函数 | ||
| C. | 偶函数,在(-∞,0)上是减函数 | D. | 偶函数,在(-∞,0)上是增函数 |
7.已知A={x|x+1>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |