题目内容
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为2x+y=0,一个焦点为($\sqrt{5}$,0),则双曲线的离心率为$\sqrt{5}$.分析 根据题意,结合双曲线的标准方程分析可得$\frac{b}{a}$=2,即b=2a,又由其焦点的坐标可得c2=b2+a2=5,联立解可得a、b的值,进而可得c的值,由离心率计算公式计算可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,其焦点在x轴上,
则其渐近线方程为y=±$\frac{b}{a}$x,
又由该双曲线的一条渐近线方程为2x+y=0,
则有$\frac{b}{a}$=2,即b=2a,
又由其一个焦点为($\sqrt{5}$,0),则有c2=b2+a2=5,
解可得a=1,b=2;
故c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$;
则其离心率e=$\frac{c}{a}$=$\sqrt{5}$;
故答案为:$\sqrt{5}$.
点评 本题考查双曲线的几何性质,关键是利用待定系数法求出双曲线的标准方程.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
12.设p:实数x,y满足(x-2)2+(y-2)2≤8,q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.已知抛物线${x^2}=-4\sqrt{5}y$的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}=1(a∈R)$的一个焦点重合,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±4x | C. | $y=±\frac{1}{4}x$ | D. | $y=±\frac{1}{2}x$ |
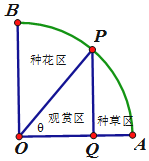 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 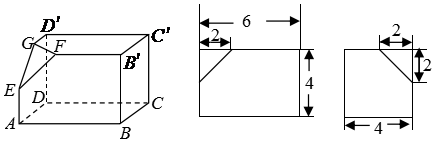
 如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.
如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.