题目内容
17.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{A{A_1}}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{BM}$可表示为( )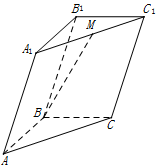
| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
分析 利用向量的三角形法则、多边形法则、向量共线定理即可得出.
解答 解:$\overrightarrow{BM}$=$\overrightarrow{BA}$+$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}M}$=$-\overrightarrow{AB}$+$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}\overrightarrow{AC}$
=$-\overrightarrow{AB}$+$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}(\overrightarrow{BC}-\overrightarrow{BA})$=$-\frac{1}{2}\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{BC}$+$\overrightarrow{A{A}_{1}}$
=-$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$,
故选:A.
点评 本题考查了向量的三角形法则、多边形法则、向量共线定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
7.已知A={x|x+1>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
12.设p:实数x,y满足(x-2)2+(y-2)2≤8,q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.为了得到函数y=3cos2x的图象,只需将函数$y=3cos(2x+\frac{π}{2})$的图象上每一个点( )
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
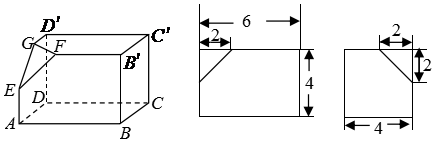
 如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.
如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.