题目内容
16.已知幂函数$f(x)={(m-1)^2}{x^{{m^2}-4m+2}}$在(0,+∞)上单调递增,函数g(x)=2x-t,?x1∈[1,6)时,总存在x2∈[1,6)使得f(x1)=g(x2),则t的取值范围是( )| A. | ∅ | B. | t≥28或t≤1 | C. | t>28或t<1 | D. | 1≤t≤28 |
分析 根据幂函数的定义以及函数的单调性求出f(x)的解析式,分别求出f(x),g(x)的值域,问题转化为[1,36)⊆[2-t,64-t),求出t的范围即可.
解答 解:由f(x)是幂函数得:m=0或2,
而$f(x)={(m-1)^2}{x^{{m^2}-4m+2}}$在(0,+∞)上单调递增,
则f(x)=x2,
x∈[1,6)时,f(x)∈[1,36),
x∈[1,6)时,g(x)∈[2-t,64-t),
若?x1∈[1,6)时,总存在x2∈[1,6)使得f(x1)=g(x2),
则[1,36)⊆[2-t,64-t),
故$\left\{\begin{array}{l}{2-t≤1}\\{64-t≥36}\end{array}\right.$,解得:1≤t≤28,
故选:D.
点评 本题考查了幂函数的定义以及函数的单调性问题,考查求函数的值域问题以及集合的包含关系,是一道中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
7.已知A={x|x+1>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
6.为了得到函数y=3cos2x的图象,只需将函数$y=3cos(2x+\frac{π}{2})$的图象上每一个点( )
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
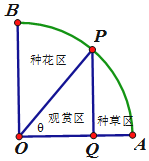 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 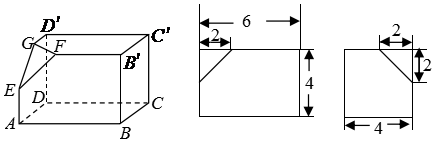
 如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.
如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.