题目内容
3.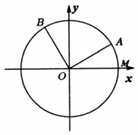 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.(Ⅰ)若α=$\frac{π}{6}$,求点A,B的坐标;
(Ⅱ)若点A的坐标为($\frac{4}{5}$,m),求sinα-sinβ的值.
分析 (Ⅰ)若α=$\frac{π}{6}$,直接利用三角函数的定义求点A,B的坐标;
(Ⅱ)若点A的坐标为($\frac{4}{5}$,m),则sinα=$\frac{3}{5}$,cosα=sinβ=$\frac{4}{5}$,即可求sinα-sinβ的值.
解答 解:(Ⅰ)若α=$\frac{π}{6}$,则点A($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(Ⅱ)若点A的坐标为($\frac{4}{5}$,$\frac{3}{5}$),则sinα=$\frac{3}{5}$,cosα=sinβ=$\frac{4}{5}$,
∴sinα-sinβ=-$\frac{1}{5}$.
点评 本题考查任意角的三角函数的定义、诱导公式的应用,比较基础.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
13.已知幂函数f(x)的图象过点$(2,\frac{{\sqrt{2}}}{2})$,则f(x)是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
14.若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的( )
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
12.设p:实数x,y满足(x-2)2+(y-2)2≤8,q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.命题“对任意实数x∈[2,3],关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是( )
| A. | a≥9 | B. | a≤9 | C. | a≤8 | D. | a≥8 |
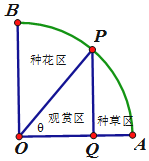 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP