题目内容
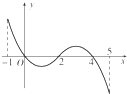 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 1.5 | 2 | 1 |
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a最多有4个零点.
其中正确命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:导数的综合应用,简易逻辑
分析:由f(x)的导函数y=f′(x)的图象如图所示,可得:函数f(x)在区间[-1,0]上单调递增;在区间[0,2]上单调递减;在区间[2,4]上单调递增;在区间[4,5]上单调递减.结合表格可得函数f(x)的图象,进而判断出答案.
解答:
解:由f(x)的导函数y=f′(x)的图象如图所示,可得:函数f(x)在区间[-1,0]上单调递增;在区间[0,2]上单调递减;在区间[2,4]上单调递增;在区间[4,5]上单调递减.结合表格可得函数f(x)的图象:
由图象可得: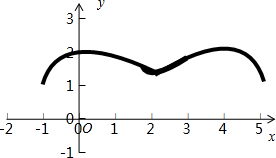
①函数f(x)的值域为[1,2],正确;
②函数f(x)在[0,2]上是减函数,正确;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,因此不正确;
④当1<a<2时,函数y=f(x)-a最多有4个零点,正确.
综上可得:正确命题的个数为:3.
故选:D.
由图象可得:

①函数f(x)的值域为[1,2],正确;
②函数f(x)在[0,2]上是减函数,正确;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,因此不正确;
④当1<a<2时,函数y=f(x)-a最多有4个零点,正确.
综上可得:正确命题的个数为:3.
故选:D.
点评:本题考查了利用导数研究函数的单调性图象与性质,考查了推理能力与数形结合的能力,属于中档题.

练习册系列答案
相关题目
若△PAB是圆C:(x-2)2+(y-2)2=4的内接三角形,且PA=PB,∠APB=120°,则线段AB的中点的轨迹方程为( )
| A、(x-2)2+(y-2)2=1 |
| B、(x-2)2+(y-2)2=2 |
| C、(x-2)2+(y-2)2=3 |
| D、x2+y2=1 |
| ∫ | 2 -2 |
| A、2e2-2 |
| B、2e2 |
| C、e2-e-2 |
| D、e2+e-2-2 |
数列{an}是公差不为零的等差数列,其前n项和为Sn,若记数据a1,a2,a3,…,a2015的方差为λ1,数据
,
,
,…,
的方差为λ2,k=
.则( )
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| λ1 |
| λ2 |
| A、k=4. |
| B、k=2. |
| C、k=1. |
| D、k的值与公差d的大小有关. |