题目内容

∫
2
-2
e|x|dx=（　　）
A、2e2-2
B、2e2
C、e2-e-2
D、e2+e-2-2
考点：定积分
专题：导数的概念及应用
分析：求出被积函数的导函数，然后分别代入积分上限和积分下限后作差得答案．
解答： 解：
∫
2
-2
e|x|dx=
∫
0
-2
e-xdx
+∫
2
0
exdx=(-e-x)
|
0
-2
+ex
|
2
0
=-e0-（-e2）+e2-e0=2e2-2．
故选：A．
点评：本题考查了定积分，关键是求出被积函数的导函数，是基础题．
练习册系列答案
相关题目
设
OA
=（1，-2），
OB
=（a，-1），
OC
=（-b，0）），（a＞0，b＞0，O为坐标原点），若A，B，C三点共线，则a与b的关系式为
 
1
a
+
2
b
 的最小值是
 
．
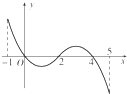已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．
x-10245
f（x）121.521
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a最多有4个零点．
其中正确命题的个数为（　　）
A、0B、1C、2D、3
求正弦函数y=sinx在0到
π
6
之间及
π
3
到
π
2
之间的平均变化率，并比较它们的大小．
已知m是非零常数，且f（x+m）=
1+f(x)
1-f(x)
，试判断f（x）是否为周期函数，若是，求出它的一个周期T；若不是，请说明理由．
以极点为原点，以极轴为x轴正半轴建立平面直角坐标系，已知曲线C的极坐标方程为ρ=10，曲线C′的参数方程为
x=3+5cosα
y=-4+5sinα
（α为参数）．
（I）判断两曲线的位置关系；
（Ⅱ）若直线l与曲线C和C′均相切，求直线l的极坐标方程．
各棱长都等于a的四面体ABCD中，设G为BC的中点，E为△ACD内的动点（含边界），且GE∥平面ABD，若线段GE长度的最小值为
3
2
，则a的值为（　　）
A、1
B、
3
C、2
D、2
3
在（1-x）5的展开式中，x2的系数为
 
（用数字作答）
函数f（x）=2x-tanx在（-
π
2
，
π
2
）上的图象大致是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网