题目内容
数列{an}是公差不为零的等差数列,其前n项和为Sn,若记数据a1,a2,a3,…,a2015的方差为λ1,数据
,
,
,…,
的方差为λ2,k=
.则( )
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| λ1 |
| λ2 |
| A、k=4. |
| B、k=2. |
| C、k=1. |
| D、k的值与公差d的大小有关. |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:分别计算平均数与方差,即可得出结论.
解答:
解:由题意,数据a1,a2,a3,…,a2015的平均数为
=a1008,
所以λ1=
[(a1-a1008)2+(a2-a1008)2+…+(a2015-a1008)2]=
•(12+22+…+10072).
数据
,
,
,…,
的平均数为a1+
d,
所以λ2=
[(a1-a1-
d)2+(a2-a1-
d)2+…+(a2015-a1-
d)2]=
•(12+22+…+10072).
所以k=
=2,
故选:B.
| S2015 |
| 2015 |
所以λ1=
| 1 |
| 2015 |
| 2 |
| 2015 |
数据
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| 1007 |
| 2 |
所以λ2=
| 1 |
| 2015 |
| 1007 |
| 2 |
| 1007 |
| 2 |
| 1007 |
| 2 |
| 1 |
| 2015 |
所以k=
| λ1 |
| λ2 |
故选:B.
点评:本题考查等差数列的通项与求和,考查平均数与方差的计算,考查学生的计算能力,正确计算是关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
设向量
=(m-2,m+3),
=(2m+1,m-2),若
与
的夹角大于90°,则实数m的取值范围是( )
| a |
| b |
| a |
| b |
A、(-
| ||
B、(-∞,-
| ||
C、(-2,
| ||
D、(-∞,2)∪(
|
函数f(x)=2x-tanx在(-
,
)上的图象大致是( )
| π |
| 2 |
| π |
| 2 |
A、 |
B、 |
C、 |
D、 |
复数z=
+ai(a∈R且a≠0)对应的点在复平面内位于( )
| 1 |
| a |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
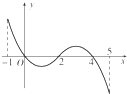 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.