题目内容

已知函数f（x）=13-2cos（5x+
π
6
），求f（x）的最值及对应x的值．
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：由条件根据余弦函数的图象特征、余弦函数的定义域和值域，求得f（x）的最值及对应x的值．
解答： 解：对于函数f（x）=13-2cos（5x+
π
6
），当5x+
π
6
=2kπ，k∈z，即x=
2kπ
5
-
π
30
，k∈z时，cos（5x+
π
6
）取得最大值为1，f（x）取得最小值为13-2=11；
当5x+
π
6
=2kπ+π，k∈z，即 x=
2kπ
5
+
π
6
，k∈z时，cos（5x+
π
6
）取得最小值为-1，f（x）取得最大值为13+2=13．
综上可得，f（x）的最小值为11，对应的x值为x=
2kπ
5
-
π
30
，k∈z；f（x）的最大值为13，对应的x值为x=
2kπ
5
+
π
6
，k∈z．
点评：本题主要考查余弦函数的定义域和值域，余弦函数的图象特征，属于基础题．
练习册系列答案
相关题目
若变量x，y满足约束条件
x≥1
y≥x
3x+2y≤15
，则w=4x•2y的最大值是
 
．
已知函数f（x）=cos（2x-
π
3
）+sin2x-cos2x+
2
．
（1）求函数f（x）的最小正周期；
（2）若存在t∈[
π
12
，
π
3
]满足[f（t）]2-2
2
f（t）-m＞0，求实数m的取值范围；
（3）对任意的x1∈[-
π
6
，
π
3
]，是否存在唯一的x2∈[-
π
6
，
π
3
]，使f（x1）•f（x2）=1成立，请说明理由．
将函数y=
3
cosx+sinx（x∈R）的图象向左平移α（α＞0，且α值最小）个单位长度后，所得到的图象关于y轴对称，则tanα的值是（　　）
A、
2
B、
3
3
C、
3
D、
2
2
设函数g（x）=（x+1）ln（x+1）-x，f（x）=a（x+1）2•ln（x+1）+bx，曲线y=f（x）在原点（0，0）处的切线方程为y=0，且经过点（e-1，e2-e+1）．
（1）求y=f（x）的表达式，并证明：当x≥0时，g（x）≥0；
（2）若当x≥0时，f（x）≥mx2恒成立，求实数m的取值范围．
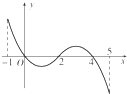已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．
x-10245
f（x）121.521
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a最多有4个零点．
其中正确命题的个数为（　　）
A、0B、1C、2D、3
已知a，b，c为正实数．
（I）若ab（a+b）=2，求a+b的最小值；
（Ⅱ）若abc（a+b+c）=1，求（a+b）（b+c）的最小值．
已知m是非零常数，且f（x+m）=
1+f(x)
1-f(x)
，试判断f（x）是否为周期函数，若是，求出它的一个周期T；若不是，请说明理由．
设向量
a
=（m-2，m+3），
b
=（2m+1，m-2），若
a
与
b
的夹角大于90°，则实数m的取值范围是（　　）
A、（-
4
3
，2）
B、（-∞，-
4
3
）∪（2，+∞）
C、（-2，
4
3
）
D、（-∞，2）∪（
4
3
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网