题目内容

已知：cosA=cosθsinC，cosB=sinθsinC，（C≠kπ，k∈Z）求sin2A+sin2B+sin2C 的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由题设条件可求得cosθ和sinθ，平方相加利用二倍角公式进行化简，最后可求得sin2A+sin2B+sin2C 的值．
解答： 解：由cosA=cosθsinC，cosB=sinθsinC，（C≠kπ，k∈Z），可得cosθ=
cosA
sinC
，sinθ=
cosB
sinC
，
平方相加可得 cos2A+cos2B=sin2C，即
1+cos2A
2
+
1+cos2B
2
=sin2C，
∴1+（1-2sin2A）+1+（1-2sin2B）=2sin2C，∴sin2A+sin2B+sin2C=2．
点评：本题主要考查了三角函数恒等式的证明．证明的关键是从条件与要证的结论之间的联系入手，将结论中的sin2B、sin2C都统一成角A的三角函数．
练习册系列答案
相关题目
运行右面的程序框图，如果输入的x的值在区间[-2，3]内，那么输出的f（x）的取值范围是
 
将函数y=
3
cosx+sinx（x∈R）的图象向左平移α（α＞0，且α值最小）个单位长度后，所得到的图象关于y轴对称，则tanα的值是（　　）
A、
2
B、
3
3
C、
3
D、
2
2
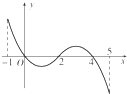已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．
x-10245
f（x）121.521
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a最多有4个零点．
其中正确命题的个数为（　　）
A、0B、1C、2D、3
已知a，b，c为正实数．
（I）若ab（a+b）=2，求a+b的最小值；
（Ⅱ）若abc（a+b+c）=1，求（a+b）（b+c）的最小值．
求正弦函数y=sinx在0到
π
6
之间及
π
3
到
π
2
之间的平均变化率，并比较它们的大小．
已知m是非零常数，且f（x+m）=
1+f(x)
1-f(x)
，试判断f（x）是否为周期函数，若是，求出它的一个周期T；若不是，请说明理由．
各棱长都等于a的四面体ABCD中，设G为BC的中点，E为△ACD内的动点（含边界），且GE∥平面ABD，若线段GE长度的最小值为
3
2
，则a的值为（　　）
A、1
B、
3
C、2
D、2
3
化简：
8-4
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网