题目内容
 如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.(Ⅰ)求证:PD⊥BC;
(Ⅱ)求直线PA与平面ABCD所成的角的正弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)由已知得BC⊥CD,从而BC⊥平面PCD,由此能证明BC⊥PD.
(Ⅱ)取DC中点O,连结OA,OP,由已知得∠PAO是直线PA与平面ABCD所成的角,由此能求出直线PA与平面ABCD所成的角的正弦值.
(Ⅱ)取DC中点O,连结OA,OP,由已知得∠PAO是直线PA与平面ABCD所成的角,由此能求出直线PA与平面ABCD所成的角的正弦值.
解答:
(Ⅰ)证明:∵平面PCD⊥平面ABCD,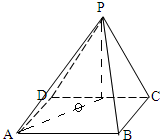
又平面PCD∩平面ABCD=CD,BC⊥CD,
∴BC⊥平面PCD,
∵PD?平面PCD,∴BC⊥PD.
(Ⅱ)解:取DC中点O,连结OA,OP,
∵PC=PD=CD=2,
∴PO⊥CD,且PO=
,
∵底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,
∴PO⊥底面ABCD,AO=
=
,AP=
=2
,
∴∠PAO是直线PA与平面ABCD所成的角,
sin∠PAO=
=
=
,
∴直线PA与平面ABCD所成的角的正弦值为
.

又平面PCD∩平面ABCD=CD,BC⊥CD,
∴BC⊥平面PCD,
∵PD?平面PCD,∴BC⊥PD.
(Ⅱ)解:取DC中点O,连结OA,OP,
∵PC=PD=CD=2,
∴PO⊥CD,且PO=
| 3 |
∵底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,
∴PO⊥底面ABCD,AO=
| 4+1 |
| 5 |
| 5+3 |
| 2 |
∴∠PAO是直线PA与平面ABCD所成的角,
sin∠PAO=
| PO |
| AP |
| ||
2
|
| ||
| 4 |
∴直线PA与平面ABCD所成的角的正弦值为
| ||
| 4 |
点评:本题考查异面直线垂直的证明,考查直线与平面所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知=
(1,2),
=(0,1),
=(-2,k),若(
+2
)⊥
,则k=( )
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
已知函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=-|x|+1,则当x∈(0,6]时,函数g(x)=f(x)-log3x的零点个数为( )
| A、5 | B、6 | C、7 | D、8 |
已知A、B是抛物线y2=4p上不同的两点,且直线AB的倾斜角为锐角,F为抛物线的焦点,且
=-4
,则直线AB的斜率为( )
| FA |
| FB |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.
如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.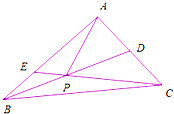 如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若
如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若