题目内容
已知F是抛物线C:y2=4x的焦点,P是抛物线C上的动点,若定点A(-1,0),则
的最小值为 .
| |PF| |
| |PA| |
考点:抛物线的简单性质
专题:函数思想,圆锥曲线的定义、性质与方程
分析:根据抛物线的定义,范围得出
=
=
=
,再利用换元法转化为
=
,0<t≤1,二次函数求解.
| |PF| |
| |PA| |
| |x+1| | ||
|
| |x+1| | ||
|
| 1 | ||||||
|
| |PF| |
| |PA| |
| 1 | ||
|
解答:
解:设P(x,y),则y=4x,
∵定点A(-1,0),F(1,0),
∴
=
=
=
设t=
,x≥0,0<t≤1,
∴
=
,0<t≤1,
当t=
时,g(t)=-4t2+4t+1最大值为2,
∴
最小值为
.
故答案为:
.
∵定点A(-1,0),F(1,0),
∴
| |PF| |
| |PA| |
| |x+1| | ||
|
| |x+1| | ||
|
| 1 | ||||||
|
设t=
| 1 |
| (x+1) |
∴
| |PF| |
| |PA| |
| 1 | ||
|
当t=
| 1 |
| 2 |
∴
| 1 | ||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考察了抛物线的定义,换元法,转化为二次函数的性质求解,属于中档题.

练习册系列答案
相关题目
若f(x)=
,则f(f(-2))=( )
|
| A、2 | B、3 | C、4 | D、5 |
已知
,
满足:|
|=3,|
|=2,则|
+
|=4,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
函数y=
,x∈[0,+∞)的值域为( )
| x-1 |
| x+1 |
| A、[-1,1) |
| B、(-1,1] |
| C、[-1,+∞) |
| D、[0,+∞) |
已知f(x)=x2-2|x|,则满足f[f(x)]=-
的实数x的个数为( )
| 1 |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
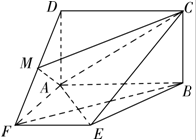 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点. 如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在Rt△ABC中,AC=1,BC=x,D为斜边AB的中点.将△BCD沿直线CD翻折.若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是
如图,在Rt△ABC中,AC=1,BC=x,D为斜边AB的中点.将△BCD沿直线CD翻折.若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是