题目内容
已知=
(1,2),
=(0,1),
=(-2,k),若(
+2
)⊥
,则k=( )
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:利用向量垂直与数量积的关系即可得出.
解答:
解:
+2
=(1,2)+2(0,1)=(1,4),
∵(
+2
)⊥
,
∴-2+4k=0,
解得k=
.
故选:D.
| a |
| b |
∵(
| a |
| b |
| c |
∴-2+4k=0,
解得k=
| 1 |
| 2 |
故选:D.
点评:本题考查了向量垂直与数量积的关系,属于基础题.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,若a2+a4+a6=12,则S7的值是( )
| A、28 | B、24 | C、21 | D、7 |
若f(x)=
,则f(f(-2))=( )
|
| A、2 | B、3 | C、4 | D、5 |
已知函数f(x)=
,则f[f(
)]的值为( )
|
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、-2 | ||
| D、3 |
函数y=
,x∈[0,+∞)的值域为( )
| x-1 |
| x+1 |
| A、[-1,1) |
| B、(-1,1] |
| C、[-1,+∞) |
| D、[0,+∞) |
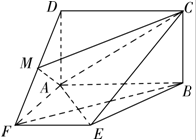 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点. 如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.