题目内容
 如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.
如图所示,平面四边形EFGH的四个顶点分别在空间四边形ABCD的四边上,且直线EH与FG相交于点P,求证:B、D、P三点共线.考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据公理1,可得直线EH?平面ABD,进而点P∈平面ABD,同理点P∈平面BCD,再由公理3可得:点P∈平面BCD∩平面ABD=BD
解答:
证明:∵E,H∈平面ABD,
∴直线EH?平面ABD,
∵点P∈直线EH,
∴点P∈平面ABD,
∵F,G∈平面BCD,
∴直线FG?平面BCD,
∵点P∈直线FG,
∴点P∈平面BCD,
∴点P∈平面BCD∩平面ABD=BD,
即B、D、P三点共线
∴直线EH?平面ABD,
∵点P∈直线EH,
∴点P∈平面ABD,
∵F,G∈平面BCD,
∴直线FG?平面BCD,
∵点P∈直线FG,
∴点P∈平面BCD,
∴点P∈平面BCD∩平面ABD=BD,
即B、D、P三点共线
点评:本题考查的知知识点是平面的基本性质及推论,熟练掌握公理1和公理3是解答的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知函数f(x)=
,则f[f(
)]的值为( )
|
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、-2 | ||
| D、3 |
函数y=
,x∈[0,+∞)的值域为( )
| x-1 |
| x+1 |
| A、[-1,1) |
| B、(-1,1] |
| C、[-1,+∞) |
| D、[0,+∞) |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、±
| ||||
D、y=±
|
 如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,底面是正方形的四棱锥P-ABCD,平面PCD⊥平面ABCD,PC=PD=CD=2.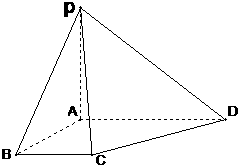 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,BC∥AD,PA⊥底面ABCD,BC=AB=1,PA=AD=2 正方体ABCD-A1B1C1D1的棱长为2,O是AC与BD的交点,E是B1B上一点,且B1E=
正方体ABCD-A1B1C1D1的棱长为2,O是AC与BD的交点,E是B1B上一点,且B1E=