题目内容
已知函数y=f（x）（x∈R）满足f（x+2）=f（x），且x∈[-1，1]时，f（x）=-|x|+1，则当x∈（0，6]时，函数g（x）=f（x）-log3x的零点个数为（ ）
| A、5 | B、6 | C、7 | D、8 |
考点：函数的零点
专题：函数的性质及应用
分析：由题意可得函数f（x）的周期为2，作图象可得答案．
解答：
解：∵函数f（x）满足f（x+2）=f（x），
∴函数f（x）的周期为2，
令g（x）=0得f（x）=log3x
又∵当x∈[-1，1]时，f（x）=-|x|+1，
∴函数y=f（x）的图象与y=log3x的图象大致如图所示，
数形结合可得图象的交点个数为：2
故答案为：2．
∴函数f（x）的周期为2，
令g（x）=0得f（x）=log3x
又∵当x∈[-1，1]时，f（x）=-|x|+1，
∴函数y=f（x）的图象与y=log3x的图象大致如图所示，
数形结合可得图象的交点个数为：2
故答案为：2．
点评：本题考查函数零点的个数，数形结合是解决本题的关键．
练习册系列答案
相关题目
下列不等式成立的是（其中a＞0且a≠1）（ ）
| A、loga5.1＜loga5.9 |
| B、1.70.3＞0.93.1 |
| C、a0.8＜a0.9 |
| D、log32.9＜log0.52.2 |
在平面直角坐标系中，已知向量
=（1，-2），
-
=（2，-3），
=（x，9），若（2
+
）∥
，则x=（ ）
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| A、-2 | B、-4 | C、-3 | D、-1 |
已知函数f（x）=
，则f[f(
)]的值为（ ）
|
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、-2 | ||
| D、3 |
如图，底面是正方形的四棱锥P-ABCD，平面PCD⊥平面ABCD，PC=PD=CD=2．
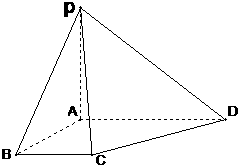如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，∠BAD=90°，BC∥AD，PA⊥底面ABCD，BC=AB=1，PA=AD=2
正方体ABCD-A1B1C1D1的棱长为2，O是AC与BD的交点，E是B1B上一点，且B1E=