题目内容
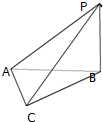 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.(1)求PA、PC与平面ABC所成的角的大小;
(2)求PA与平面PBC所成的角的正弦值;
(3)试比较∠PAC与∠PAB的正弦值的大小.
考点:直线与平面所成的角
专题:空间角
分析:(1)由PB⊥平面ABC,得∠BCP中PC与平面ABC所成的角,∠BAP中PC与平面ABC所成的角,由此能求出PA、PC与平面ABC所成的角的大小.
(2)由PB⊥平面ABC,得AC⊥PB,从而AC⊥平面PBC,∠APC为直线AP与平面PBC所成的角,由此能求出PA与平面PBC所成的角的正弦值.
(3)sin∠PAC=
,sin∠PAB=
,由此能求出∠PAC的正弦值大于∠PAB的正弦值.
(2)由PB⊥平面ABC,得AC⊥PB,从而AC⊥平面PBC,∠APC为直线AP与平面PBC所成的角,由此能求出PA与平面PBC所成的角的正弦值.
(3)sin∠PAC=
| PC |
| PA |
| PB |
| PA |
解答:
解:(1)∵PB⊥平面ABC,
∴∠BCP中PC与平面ABC所成的角,
∵PB=BC,∴∠BCP=45°,
∴PC与平面ABC所成的角为45°.
∵PB⊥平面ABC,
∴∠BAP中PC与平面ABC所成的角,
∵PB=BC=AC,∠ACB=90°,
AB=
PB,
∴tan∠BAP=
,
∴PA与平面ABC所成的角为arctan
.
(2)∵PB⊥平面ABC,∴AC⊥PB,
∵△ABC为直角三角形,PB=BC=AC,∠ACB=90°,
∴AC⊥BC,
∴AC⊥平面PBC,
∴∠APC为直线AP与平面PBC所成的角,
设PB=BC=AC=1,则PC=
,AP=
,
∴sin∠APC=
=
=
.
∴PA与平面PBC所成的角的正弦值为
.
(3)sin∠PAC=
=
=
,
sin∠PAB=
=
=
,
∴∠PAC的正弦值大于∠PAB的正弦值.
∴∠BCP中PC与平面ABC所成的角,
∵PB=BC,∴∠BCP=45°,
∴PC与平面ABC所成的角为45°.
∵PB⊥平面ABC,
∴∠BAP中PC与平面ABC所成的角,
∵PB=BC=AC,∠ACB=90°,
AB=
| 2 |
∴tan∠BAP=
| ||
| 2 |
∴PA与平面ABC所成的角为arctan
| ||
| 2 |
(2)∵PB⊥平面ABC,∴AC⊥PB,
∵△ABC为直角三角形,PB=BC=AC,∠ACB=90°,

∴AC⊥BC,
∴AC⊥平面PBC,
∴∠APC为直线AP与平面PBC所成的角,
设PB=BC=AC=1,则PC=
| 2 |
| 3 |
∴sin∠APC=
| AC |
| AP |
| 1 | ||
|
| ||
| 3 |
∴PA与平面PBC所成的角的正弦值为
| ||
| 3 |
(3)sin∠PAC=
| PC |
| PA |
| ||
|
| ||
| 3 |
sin∠PAB=
| PB |
| PA |
| 1 | ||
|
| ||
| 3 |
∴∠PAC的正弦值大于∠PAB的正弦值.
点评:本题考查角的大小的求法,考查角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目