题目内容
若对于任意x∈(-2,2)都有2x(x-a)<1成立,则a的取值范围是( )
| A、(-∞,-6) | ||
B、(
| ||
C、[
| ||
| D、(-6,+∞) |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:将不等式恒成立变形为a>x-
对于任意x∈(-2,2)恒成立,利用导数研究函数f(x)=x-
的单调性,从而得到f(x)的取值范围,即可求得实数a的取值范围.
| 1 |
| 2x |
| 1 |
| 2x |
解答:
解:∵2x(x-a)<1对于任意x∈(-2,2)恒成立,
∵2x>0,
∴2x(x-a)<1对于任意x∈(-2,2)恒成立等价于a>x-
对于任意x∈(-2,2)恒成立,
令f(x)=x-
,则f′(x)=1+
>0在(-2,2)上恒成立,
故函数f(x)在(-2,2)上为单调递增函数,
∴f(x)<f(2)=
,
∴a≥
>f(x),
∴a的取值范围是[
,+∞).
故选:C.
∵2x>0,
∴2x(x-a)<1对于任意x∈(-2,2)恒成立等价于a>x-
| 1 |
| 2x |
令f(x)=x-
| 1 |
| 2x |
| ln2 |
| 2x |
故函数f(x)在(-2,2)上为单调递增函数,
∴f(x)<f(2)=
| 7 |
| 4 |
∴a≥
| 7 |
| 4 |
∴a的取值范围是[
| 7 |
| 4 |
故选:C.
点评:本题考查了恒成立问题,对于不等式恒成立问题一般选用参变量分离法、最值法、数形结合法求解.考查了运用导数研究函数的单调性,注意导数的正负对应着函数的单调性.属于中档题.

练习册系列答案
相关题目
函数y=x(x2-1)的大致图象是( )
A、 |
B、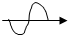 |
C、 |
D、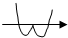 |
已知等比数列{an}的公比q=
,其前4项和S4=60,则a2等于( )
| 1 |
| 2 |
| A、8 | B、12 | C、16 | D、20 |
设a、b是非负实数,且a2+b2=4,则
( )
| ab |
| a+b+2 |
A、有最大值
| ||
B、有最小值
| ||
C、有最大值
| ||
D、有最小值
|