题目内容
已知圆C:x2+y2-x-8y+m=0,点R是直线y=x上一动点,
(1)若圆C与直线y=x相离,过动点R作圆C的切线,求切线长的最小值的平方f(m);
(2)若圆C与直线x+2y-6=0相交于P、Q两点,R(1,1)且PR⊥QR,求m的值.
(1)若圆C与直线y=x相离,过动点R作圆C的切线,求切线长的最小值的平方f(m);
(2)若圆C与直线x+2y-6=0相交于P、Q两点,R(1,1)且PR⊥QR,求m的值.
考点:圆的切线方程,圆的一般方程
专题:计算题,直线与圆
分析:(1)由圆C方程算出圆心为C(
,4)、半径r=
.根据题意,当动点R与点C直线y=x上的射影重合时切线长达到最小值,由此结合点到直线的距离公式与勾股定理加以计算,可得切线长的最小值的平方f(m);
(2)利用PQ的中垂线方程与PQ方程联解,得到PQ的中点为M(0,3).由PR⊥QR得|MP|=|MQ|=|MR|=
,算出|CM|=
并结合r2=|MQ|2+|CM|2建立关于m的等式,解之即可得到实数m的值.
| 1 |
| 2 |
|
(2)利用PQ的中垂线方程与PQ方程联解,得到PQ的中点为M(0,3).由PR⊥QR得|MP|=|MQ|=|MR|=
| 5 |
| ||
| 2 |
解答:
解:(1)圆C:x2+y2-x-8y+m=0化成标准方程,得(x-
)2+(y-4)2=
-m.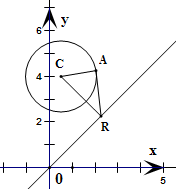
∴圆心为C(
,4),半径r=
,
又∵圆C与直线y=x相离,∴点C到直线y=x的距离大于半径r,
即d=
>
,即
>
,解得
<m<
.
根据圆切线的性质,可得当动点R与点C直线y=x上的射影重合时,
切线长达到最小值,
此时切线长l=
=
=
,
∴切线长的最小值的平方f(m)=m-
,其中
<m<
;
(2)∵圆的方程为(x-
)2+(y-4)2=
-m,圆心C(
,4),
∴过C作直线PQ垂线为:2x-y+3=0,
与x+2y-6=0联解,可得PQ的中点为M(0,3),
又∵PR⊥QR,
∴|MP|=|MQ|=|MR|=
=
,
∵|CM|=
=
,r2=|MQ|2+|CM|2,
∴
-m=5+
,解之得m=10.
| 1 |
| 2 |
| 65 |
| 4 |

∴圆心为C(
| 1 |
| 2 |
|
又∵圆C与直线y=x相离,∴点C到直线y=x的距离大于半径r,
即d=
|
| ||
|
|
7
| ||
| 4 |
|
| 81 |
| 8 |
| 65 |
| 4 |
根据圆切线的性质,可得当动点R与点C直线y=x上的射影重合时,
切线长达到最小值,
此时切线长l=
| d2-r2 |
(
|
m-
|

∴切线长的最小值的平方f(m)=m-
| 81 |
| 8 |
| 81 |
| 8 |
| 65 |
| 4 |
(2)∵圆的方程为(x-
| 1 |
| 2 |
| 65 |
| 4 |
| 1 |
| 2 |
∴过C作直线PQ垂线为:2x-y+3=0,
与x+2y-6=0联解,可得PQ的中点为M(0,3),
又∵PR⊥QR,
∴|MP|=|MQ|=|MR|=
| (1-0)2+(1-3)2 |
| 5 |
∵|CM|=
(
|
| ||
| 2 |
∴
| 65 |
| 4 |
| 15 |
| 4 |
点评:本题给出含有参数m的圆方程,在指定的条件下求m的值.着重考查了圆的标准方程、直线与圆的位置关系、点到直线的距离公式等知识,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
若对于任意x∈(-2,2)都有2x(x-a)<1成立,则a的取值范围是( )
| A、(-∞,-6) | ||
B、(
| ||
C、[
| ||
| D、(-6,+∞) |
已知函数f(x)=
,则f(-2)=( )
|
| A、0 | B、1 | C、-2 | D、-1 |