题目内容
函数y=x（x2-1）的大致图象是（ ）
A、 |
B、 |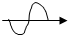
C、 |
D、 |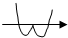
考点：函数的图象
专题：函数的性质及应用
分析：通过对函数的奇偶性进行研究，发现函数为奇函数，再考虑一些特殊值的取值，比如当0＜x＜1时，f（x）＜0，即可判断得到答案．
解答：
解：∵函数y=x（x2-1），令f（x）=x（x2-1），
则f（-x）=-x（x2-1）=-f（x），
故函数f（x）为奇函数，
又当0＜x＜1时，f（x）＜0，
综上所述，函数y=x（x2-1）的大致图象是选项A．
故选：A．
则f（-x）=-x（x2-1）=-f（x），
故函数f（x）为奇函数，
又当0＜x＜1时，f（x）＜0，
综上所述，函数y=x（x2-1）的大致图象是选项A．
故选：A．
点评：本题考查了函数的图象．研究函数图象一般从定义域、值域、单调性、对称性、恒过的定点、渐近线等方面进行研究．属于基础题．
练习册系列答案
相关题目
函数f（x）=lg（3x-1）的定义域为（ ）
A、(
| ||
B、(-∞，
| ||
C、[
| ||
| D、（0，+∞） |
设f(x)=|sinx|，若x1，x2∈[-
，
]，且f(x1)＞f(x2)，则下列结论成立的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、x1＜x2 |
| B、x1+x2＞0 |
| C、x1＞x2 |
| D、x12＞x22 |
如图几何体上半部分是母线长为5，底面圆半径为3的圆锥，下半部分是下底面圆半径为2，母线长为2的圆台，计算该几何体的表面积和体积．若对于任意x∈（-2，2）都有2x（x-a）＜1成立，则a的取值范围是（ ）
| A、（-∞，-6） | ||
B、（
| ||
C、[
| ||
| D、（-6，+∞） |