题目内容
某电视台为了宣传安徽沿江城市经济崛起的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“沿江城市带包括哪几个城市”,统计数据结果如下表:
(1)分别求出n,a,x的值;
(2)若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48]内回答正确的得奖金200元,年龄在[18,28)内回答正确的得奖金100元.主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答问题,求该家庭获得奖金ξ的分布列及数学期望(两个回答问题正确与否相互独立).
| 组数 | 分组 | 回答正确的人数 | 占本组的频率 |
| 第1组 | [18,28) | 240 | x |
| 第2组 | [28,38) | 300 | 0.6 |
| 第3组 | [38,48] | a | 0.4 |
(2)若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48]内回答正确的得奖金200元,年龄在[18,28)内回答正确的得奖金100元.主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答问题,求该家庭获得奖金ξ的分布列及数学期望(两个回答问题正确与否相互独立).
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由频率表中第2组数据可知,第2组总人数为
=500,再结合频率分布直方图能求出n,a,x的值.
(2)由题意知ξ可能的取值为0,100,200,300,分别求出相应的概率,由此能求出该家庭获得奖金ξ的分布列和Eξ.
| 300 |
| 0.6 |
(2)由题意知ξ可能的取值为0,100,200,300,分别求出相应的概率,由此能求出该家庭获得奖金ξ的分布列和Eξ.
解答:
(本题13分)
解:(1)由频率表中第2组数据可知,第2组总人数为
=500,再结合频率分布直方图可知:
n=
=1000,所以a=1000×0.02×10×0.4=80,
x=
=0.8.
(2)由题意知ξ可能的取值为0,100,200,300,父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,且P(ξ=0)=0.6×0.2=0.12,P(ξ=100)=0.6×0.8=0.48,P(ξ=200)=0.4×0.2=0,0,8P(ξ=300)=0.4×0.8=0.32,
所以该家庭获得奖金ξ的分布列为
故Eξ=0×0.12+100×0.48+200×0.08+300×0.32=160.
解:(1)由频率表中第2组数据可知,第2组总人数为
| 300 |
| 0.6 |
n=
| 500 |
| 0.05×10 |
x=
| 240 |
| 1000×0.03×10 |
(2)由题意知ξ可能的取值为0,100,200,300,父亲回答正确的概率为0.4,孩子回答正确的概率为0.8,且P(ξ=0)=0.6×0.2=0.12,P(ξ=100)=0.6×0.8=0.48,P(ξ=200)=0.4×0.2=0,0,8P(ξ=300)=0.4×0.8=0.32,
所以该家庭获得奖金ξ的分布列为
| ξ | 0 | 100 | 200 | 300 |
| P | 0.12 | 0.48 | 0.08 | 0.32 |
点评:本题考查离散型随机变量的数学期望和方差的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知a,b是不相等的正数,且a2-a+b2-b+ab=0,则a+b的取值范围是( )
A、(0,
| ||
B、(1,
| ||
C、(0,
| ||
D、(1,
|
已知f(x)=
-
,g(x)=|x-2|-2,记F(t)=
[f(x)-g(x)]dx,函数F(t)的导函数为F′(t),则函数y=F′(t),t∈(0,4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
| ∫ | t 0 |
A、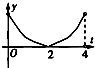 |
B、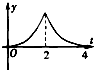 |
C、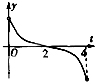 |
D、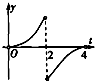 |
定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),则实数m的取值范围是( )
A、m<
| ||
B、m>
| ||
C、-1≤m<
| ||
D、
|
 函数y=f(x)的图象如图所示,那么,f(x)的定义域是
函数y=f(x)的图象如图所示,那么,f(x)的定义域是