题目内容
已知圆C:x2+y2+x-6y+m=0和直线l:x+y-3=0
(Ⅰ)求m的取值范围;
(Ⅱ)当圆C与直线l相切时,求圆C关于直线l的对称圆方程;
(Ⅲ)若圆C与直线l交于P、Q两点,是否存在m,使以PQ为直径的圆经过原点O?
(Ⅰ)求m的取值范围;
(Ⅱ)当圆C与直线l相切时,求圆C关于直线l的对称圆方程;
(Ⅲ)若圆C与直线l交于P、Q两点,是否存在m,使以PQ为直径的圆经过原点O?
考点:直线与圆的位置关系
专题:综合题,直线与圆
分析:(Ⅰ)圆C:x2+y2+x-6y+m=0可化为圆C:(x+
)2+(y-3)2=-m+
,即可求m的取值范围;
(Ⅱ)圆C与直线l相切,可得 R=d=
=
,求出C(-
,3)关于直线l的对称点,即可求圆C关于直线l的对称圆方程;
(Ⅲ)设圆方程x2+y2+x-6y+m+λ(x+y-3)=0,可得圆心(-
,-
),代入直线l得λ=-
,圆过原点得m=3λ=-
,即可得出结论.
| 1 |
| 2 |
| 37 |
| 4 |
(Ⅱ)圆C与直线l相切,可得 R=d=
|-
| ||
|
| 1 | ||
2
|
| 1 |
| 2 |
(Ⅲ)设圆方程x2+y2+x-6y+m+λ(x+y-3)=0,可得圆心(-
| 1+λ |
| 2 |
| λ-6 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(Ⅰ)圆C:x2+y2+x-6y+m=0可化为圆C:(x+
)2+(y-3)2=-m+
,
∵-m+
>0,
∴m<
-------------3分
(Ⅱ)圆C:x2+y2+x-6y+m=0,
∴圆心C(-
,3),
∵圆C与直线l相切,
∴R=d=
=
,-------------5分
设C(-
,3)关于直线l的对称点M(a,b),则
,∴a=0,b=
,-------------7分
故所求圆的方程为:x2+(y-
)2=
------------8分
(Ⅲ)设圆方程x2+y2+x-6y+m+λ(x+y-3)=0,可得圆心(-
,-
)
代入直线l得λ=-
,
圆过原点得m=3λ=-
,检验满足,
故存在m=-
,使以PQ为直径的圆经过原点O.------------12分
| 1 |
| 2 |
| 37 |
| 4 |
∵-m+
| 37 |
| 4 |
∴m<
| 37 |
| 4 |
(Ⅱ)圆C:x2+y2+x-6y+m=0,
∴圆心C(-
| 1 |
| 2 |
∵圆C与直线l相切,
∴R=d=
|-
| ||
|
| 1 | ||
2
|
设C(-
| 1 |
| 2 |
|
| 7 |
| 2 |
故所求圆的方程为:x2+(y-
| 7 |
| 2 |
| 1 |
| 8 |
(Ⅲ)设圆方程x2+y2+x-6y+m+λ(x+y-3)=0,可得圆心(-
| 1+λ |
| 2 |
| λ-6 |
| 2 |
代入直线l得λ=-
| 1 |
| 2 |
圆过原点得m=3λ=-
| 3 |
| 2 |
故存在m=-
| 3 |
| 2 |
点评:本题考查直线与圆的性质的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知f(x)=
-
,g(x)=|x-2|-2,记F(t)=
[f(x)-g(x)]dx,函数F(t)的导函数为F′(t),则函数y=F′(t),t∈(0,4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
| ∫ | t 0 |
A、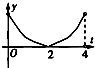 |
B、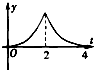 |
C、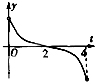 |
D、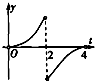 |
定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),则实数m的取值范围是( )
A、m<
| ||
B、m>
| ||
C、-1≤m<
| ||
D、
|