题目内容
数列1,
,
,
,
,
,
,
,
,
,…前130项的和等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
A、15
| ||
B、15
| ||
C、15
| ||
D、15
|
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:由题意可知,此数列由一个1,两个
,3个
…组成,欲求前130项的和,需求自然数列前n项和不大于130时的最大n值,即可得出结论..
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:因为1+2+3+…+n=
n(n+1),
由
n(n+1)≤130,得n的最大值为15,
即最后一个
是数列的第120项,
共有10项,
所以,前130项的和等于15+
=15
.
故选B.
| 1 |
| 2 |
由
| 1 |
| 2 |
即最后一个
| 1 |
| 15 |
| 1 |
| 16 |
所以,前130项的和等于15+
| 10 |
| 16 |
| 5 |
| 8 |
故选B.
点评:本题考查数列的应用.解题时要认真观察,发现规律,利用等差数列知识解答.易错点是找不到规律,导致出错.

练习册系列答案
相关题目
已知f(x)=
-
,g(x)=|x-2|-2,记F(t)=
[f(x)-g(x)]dx,函数F(t)的导函数为F′(t),则函数y=F′(t),t∈(0,4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
| ∫ | t 0 |
A、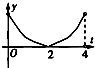 |
B、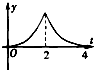 |
C、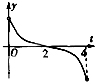 |
D、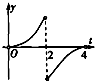 |
定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),则实数m的取值范围是( )
A、m<
| ||
B、m>
| ||
C、-1≤m<
| ||
D、
|
某商场经营的某种包装的大米质量服从正态分布N(10,0.12)(单位:kg),任选一袋这种大米,则质量在9.810.2kg的概率是( )
| A、0.9544 |
| B、0.9744 |
| C、0.6826 |
| D、0.5 |