题目内容
9.若(1+x)(a-x)6=a0+a1x+a2x2+…+a7x7,其中a=${∫}_{0}^{π}$(sinx-cosx)dx,则a0+a1+a2+…+a6的值为1.分析 首先求出a,然后对x赋值,求系数和.
解答 解:a=${∫}_{0}^{π}$(sinx-cosx)dx=(-cosx-sinx)|${\;}_{0}^{π}$=-cosπ-sinπ+cos0+sin0=2,
所以(1+x)(2-x)6=a0+a1x+a2x2+…+a7x7,其中a7=1,令x=1,得到a0+a1+a2+…+a6=2-1=1;
故答案为:1.
点评 本题考查了二项式定理的运用以及利用赋值法求展开式的系数.

练习册系列答案
相关题目
12.已知复数$z=\frac{2-i}{2+i}-\frac{2+i}{2-i}$,则z=( )
| A. | -$\frac{8i}{5}$ | B. | $\frac{8i}{5}$ | C. | $-\frac{6}{5}$ | D. | $\frac{6}{5}$ |
1.调查者通过询问64名男女大学生在购买食品时是否看营养说明,得到的数据如表所示:
问大学生的性别与是否看营养说明之间有没有关系?
附:参考公式与数据:χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$.当χ2>3.841时,有95%的把握说事件A与B有关;当χ2>6.635时,有99%的把握说事件A与B有关;当χ2≤3.841时,有95%的把握说事件A与B是无关的.
| 看营养说明 | 不看营养说明 | 合计 | |
| 男大学生 | 26 | 6 | 32 |
| 女大学生 | 14 | 18 | 32 |
| 合计 | 40 | 24 | 64 |
附:参考公式与数据:χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$.当χ2>3.841时,有95%的把握说事件A与B有关;当χ2>6.635时,有99%的把握说事件A与B有关;当χ2≤3.841时,有95%的把握说事件A与B是无关的.
19.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
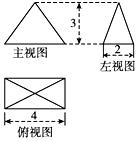

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |