题目内容
4.已知函数f(x)=x-1-alnx(a<0).(1)讨论f(x)的单调性;
(2)若对任意x1,x2∈(0,1],且x1≠x2,都有$|f({x_1})-f({x_2})|<4|\frac{1}{x_1}-\frac{1}{x_2}|$,求实数a的取值范围.
分析 (1)求出函数的导数,根据a的范围,求出导函数的符号,从而求出函数的单调区间,
(2)将问题转化为x2-ax-4≤0在x∈(0,1]时恒成立,而函数y=x-$\frac{4}{x}$在区间(0,1]上是增函数,所以y=x-$\frac{4}{x}$的最大值为-3,从而求出a的范围.
解答 解:(1)函数f(x)的定义域(0,+∞),f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,
当a<0时,f'(x)>0恒成立,此时,函数f(x)在(0,+∞)上是增函数;
(2)当a<0时,函数f(x)在(0,1]上是增函数,
又函数y=$\frac{1}{x}$在(0,1]上是减函数,不妨设0<x1<x2≤1,
则|f(x1)-f(x2)|=f(x2)-f(x1),|$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$|=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$,
所以|f(x1)-f(x2)|<4|$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$|等价于f(x2)-f(x1)<$\frac{4}{{x}_{1}}$-$\frac{4}{{x}_{2}}$,
即f(x2)+$\frac{4}{{x}_{2}}$<f(x1)+$\frac{4}{{x}_{1}}$,
设h(x)=f(x)+$\frac{4}{x}$=x-1-alnx+$\frac{4}{x}$,
则|f(x1)-f(x2)|<4|$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$|等价于函数h(x)在区间(0,1]上是减函数.
于是h′(x)=1-$\frac{a}{x}$-$\frac{4}{{x}^{2}}$=$\frac{{x}^{2}-ax-4}{{x}^{2}}$≤0即x2-ax-4≤0在x∈(0,1]时恒成立,
从而a≥x-$\frac{4}{x}$在x∈(0,1]上恒成立,
而函数y=x-$\frac{4}{x}$在区间(0,1]上是增函数,
所以y=x-$\frac{4}{x}$的最大值为-3.
于是a≥-3,又a<0,所以a∈[-3,0).
点评 本题考查了函数的单调性,函数的最值问题,考查导数的应用,求参数的范围,考查转化思想,是一道综合题.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案| A. | $\frac{6}{5}$i | B. | $\frac{8i}{5}$ | C. | -$\frac{8i}{5}$ | D. | -$\frac{6}{5}$i |
| A. | $\overline{x}$=μ | B. | $\overline{x}$≈μ | C. | μ是$\overline{x}$的估计值 | D. | $\overline{x}$是μ的估计值 |
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
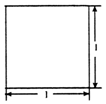 若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )| A. | 6π或5π | B. | 3π或5π | C. | 6π | D. | 5π |