题目内容
14.一个频率分布表(样本容量为30)不小心被损坏了一部分,只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,60)内的数据个数为( )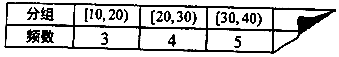
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
分析 由样本中数据在[20,60)上的频率为0.8,求出样本中数据在[20,60)上的频数为24,由此能估计样本在[40,60)内的数据个数.
解答 解:∵一个频率分布表(样本容量为30)不小心被损坏了一部分,
只记得样本中数据在[20,60)上的频率为0.8,
∴样本中数据在[20,60)上的频数为:30×0.8=24,
∴估计样本在[40,60)内的数据个数为:24-4-5=15.
故选:B.
点评 本题考查频数的求法,涉及到频率分布表等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17.已知i是虚数单位,复数z满足(1-i)z=i,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
19.有下列一列数:1,8,27,64, ,216,343,…,按照此规律,横线中的数应为( )
| A. | 75 | B. | 100 | C. | 125 | D. | 150 |
6.已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=3,则点(a,b)所在的直线为( )
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
3.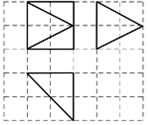 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
4.若tan($\frac{α}{2}$+$\frac{π}{4}$)=-2,则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |